La régression linéaire simple
Le prestige social des professions
Une grande partie des questions que nous nous posons en psychologie revient à se demander quelle est la forme que prend la relation entre deux variables. Par exemple, imaginons que nous intéressons à la question de savoir ce qui peut bien faire le prestige d'une profession (Fox, 2016, 2020). Nous pourrions par exemple nous demander si ce n'est pas associé au niveau d'étude exigé pour pouvoir l'exercer. Dans l'atelier qui suit, on essaie de préciser ce que l'on peut entendre par lien.
Atelier 1 : traduction d'une hypothèse de relation en fonction
- Formulez en mots comment années d'études et prestige social d'une profession pourraient être liés.
- Sur la graphique interactif ci-contre, déplacez les points pour obtenir une représentation fonctionnelle dont l'allure vous paraît traduire l'hypothèse verbale.
- Y a-t-il plusieurs solutions ?
- Y a-t-il des formes qui seraient contradictoires avec l'hypothèse ?
-
expand_moreEn résumé
En répondant aux questions de cet exercice, on peut dire que :
- s'il existe une relation entre nombres d'années d'études requis et prestige social associé à une profession, cette relation doit être croissante : plus les études sont longues, plus la profession doit être prestigieuse,
- quand on essaie de traduire cette hypothèse de relation croissante en représentation graphique fonctionnelle, on doit s'assurer que, de la gauche vers la droite, chaque point est à un niveau plus élevé que le précédent,
- néanmoins, on constate rapidement qu'il n'y a pas qu'une seule manière de faire cela. L'ensemble des possibilités est l'ensemble des fonctions croissantes, et elles peuvent prendre des formes très différentes (avec des ralentissements, avec un plafonnement, avec des paliers, etc.).
- Par contre, on peut exclure des candidats possibles toute fonction décroissante ou localement décroissante (si l'hypothèse est juste).
- Une partie de la difficulté en modélisation statistique, au-delà du choix d'un modèle de distribution, est de faire un choix de fonction de lien. Celui-ci peut-être pragmatique ou arbitraire, quand on n'a pas d'argument théorique (une hypothèse linéaire par exemple), ou justifié (par exemple un effet de plafond parce que la variable de prestige est bornée).
Un modèle de proportionnalité
Dans ce contexte de l'étude d'une relation entre deux variables, on appelle variable dépendante (notée $Y$) la variable qui est objet d'étude (le prestige), et variable indépendante (notée $X$) celle dont on suppose qu'elle construit (au moins partiellement) le phénomène prestige.
Le plus simple de tous les modèles de relation est le modèle linéaire ou proportionnel : $$Y=\beta_{0}+\beta_{1}X$$ avec $\beta_{0}$ et $\beta_{1}$ deux nombres inconnus appelés paramètres du modèle. La représentation graphique de ce modèle est celle d'une droite, dont les caractéristiques sont gouvernées par ces deux paramètres. On étudie ces effets dans l'atelier suivant.
Atelier 2 : interprétation des paramètres d'un modèle linéaire
Mode d'emploi : les deux paramètres $\beta_0$ et $\beta_1$ peuvent être réglés précisément en saisissant une valeur dans les boites de texte, ou modifiés continûment en utilisant les curseurs.
-
expand_moreEn résumé
En répondant aux questions de cet exercice, on comprend que :
- le paramètre $\beta_0$ règle la position verticale de la droite, c'est-à-dire une valeur minimale de prestige qui concerne toutes les professions, quel que soit le nombre d'années d'études requis. Son interprétation est encore plus simple si on observe que c'est la valeur que prend $Y$ quand $X$ est nul. C'est donc le prestige de base, associé à une profession qui ne demanderait aucun diplôme. Sur le graphique, cette valeur correspond à l'endroit où la droite coupe l'axe des $Y$, ce qui justifie qu'on l'appelle « ordonnée à l'origine » en français (ou intercept en anglais).
- le paramètre $\beta_1$ règle l'angle que fait la droite avec l'axe des $X$. Il module la croissance du prestige en fonction des années d'études. On constate dans la formule (1) qu'il correspond à l'augmentation du prestige pour une année d'études en plus.
- les limites du modèle linéaire apparaissent quand la variable dépendante est bornée : on voit la droite sortir du domaine de la variable. Le choix d'un modèle linéaire est donc dépendant des propriétés de la mesure étudiée.
Estimation des paramètres inconnus d'un modèle linéaire

En pratique, on ne connaît pas les paramètres vrais d'un modèle linéaire, en supposant qu'il soit un modèle acceptable de la situation étudiée. On doit donc les estimer.
De plus, dans la réponse à un questionnaire sur le prestige d'une profession, de nombreuses autres variables que la seule caractéristique « niveau d'études exigé » sont susceptibles d'intervenir dans la réponse des personnes interrogées (motivation, fatigue, niveau d'information...). Ces variables vont se mélanger dans la réponse finale fournie. C'est ce qu'on appelle l'erreur de mesure. On ne s'attend donc pas, même si une relation simplement linéaire existe dans la perception sociale entre niveau d'études et prestige, à avoir les points (niveau, prestige) tous parfaitement alignés.
Dans la figure ci-dessus, deux modèles sont représentés : un modèle de droite cible $M_1$, que nous cherchons à ajuster au mieux aux données observées, et un modèle de référence $M_0$, qui n'a pas d'autre intérêt que de servir de base de comparaison. Ce modèle $M_0$ représente l'hypothèse qui affirme qu'il n'y a en réalité aucune relation entre années d'études et prestige d'une profession. Pour ces deux modèles, nous pouvons examiner la façon dont ils s'ajustent aux données, et retenir celui qui nous paraît le mieux ajusté. C'est ce que la notion de déviance permet de mesurer.
Notion de déviance
On peut mesurer l'écart entre les données observées et n'importe quel modèle de droite en calculant toutes les différences entre chaque réponse observée $Y_i$ et la valeur correspondante $\hat{Y}_i$ (appelée prévision) telle qu'elle est modélisée par le droite, sous la forme de ce qu'on appelle les résidus du modèle ou écarts $e_i$ (pour une observation $i$ donnée, $i=1,\dots,N$) : $$e_i=Y_i-\hat{Y}_i$$
On réunit tous ces écarts dans une mesure globale appelée déviance, qui fait la somme de tous les écarts au carré : $$D_{1}=\sum_{i=1}^{N}(Y_{i}-\hat{Y}_{i})^{2}$$ On note que d'élever au carré tous ces écarts permet d'éviter de voir s'annuler les sommes d'écarts positifs et négatifs potentiellement. Cette mesure est exactement égale à 0 si tous les points sont parfaitement alignés le long de la droite, et d'autant plus grande que les points sont dispersés autour de la droite.
La mesure de la déviance sert à deux choses :
- Estimer les paramètres $\beta_0$ et $\beta_1$ : pour obtenir des valeurs satisfaisantes de ces paramètres, on cherche celles qui rendent la déviance la plus faible possible.
- Comparer des modèles concurrents : pour choisir un modèle parmi plusieurs concurrents, on va regarder et comparer leurs déviances. On retiendra celui qui a, de façon significative (voir plus loin), la déviance la plus faible. On inclura systématiquement dans cette comparaison le modèle constant $M_0$ (voir la ligne horizontale grise sur figure ci-dessus), encore appelé modèle nul, qui permet (par rejet) d'affirmer l'existence d'une relation (quelle qu'elle soit). On voit sur la figure que s'il existe réellement une relation de proportionnalité, ce modèle qui ne suppose pas de lien aura toujours une déviance plus élevée que n'importe quel autre modèle.
Atelier 3 : découverte de l'interface de régression linéaire
L'interface ci-dessous permet d'estimer automatiquement les paramètres d'un modèle de relation linéaire (ou de proportionnalité) entre deux variables, par maximisation d'une vraisemblance gaussienne.
Au cours de l'exercice, vous parcourerez les onglets de l'interface dans cet ordre :
- Dans l'onglet Fichiers, ouvrez le fichier exemple prestige.csv, que vous aurez au préalable téléchargé et enregistré sur votre machine.
- Dans l'onglet Données, observez le format du tableau chargé.
- Dans l'onglet Modèle, remplissez les champs VD et VI en fonction de la question que nous nous posons, et donnez un nom au modèle.
- Cliquez sur le bouton « Estimer » pour obtenir les estimations, à lire dans l'onglet Résultats, rubrique « coefficients ».
- Examinez l'allure de la fonction linéaire estimée, dans l'onglet Graphiques.
Puis répondez aux questions ci-contre.
Dans cette atelier, vous avez exploré les fonctionnalités basiques de l'interface de modélisation linéaire. Nous allons explorer des fonctionnalités plus avancées dans les sections et chapitres qui suivent.
Modèle de distribution sur l'erreur
Nous avons supposé une relation de proportionnalité entre éducation et prestige : cette relation
est-elle
exacte ? D'après la feuille de résultats, le calculateur a estimé cette relation par l'équation de
droite
:
$$Y=-10.8409+5.3884X$$
Mais deux points du graphique ont exactement même abscisse $x=9.93$, pour deux ordonnées différentes :
$y_{1}=23.3$ et $y_{2}=50.2$ (repérez-les dans l'onglet Graphiques). Que peut donc représenter
leur
commune valeur modèle $\hat{y}=-10.8409+(5.3884\times9.93)=42.66591$, lue sur la droite ?
Nous comprenons à travers cet exemple qu'un modèle mathématique de la forme $Y=\beta_{0}+\beta_{1}X$
se trompe nécessairement sur des données imparfaites. Pour une valeur $X=x$ fixée, nous
pouvons avoir $Y=y_{1},y_{2},...$. On appelle résidu de l'observation $i$ ($i=1,...,N$)
la valeur d'erreur :
$$e_{i}=y_{i}-(\beta_{0}+\beta_{1}x_{i}).$$
Pour bien distinguer ce que l'on observe de ce que prévoit le modèle, on note $\hat{Y}$ la
prévision faite par le modèle. Données empiriques et prévision du modèle sont réunies
par
la relation :
$$\begin{array}{ccccc}
Y & = & \hat{Y} & + & \epsilon\\
& = & (\beta_{0}+\beta_{1}X) & + & \epsilon\\
\mbox{Score} & = & \mbox{Prévision} & + & \mbox{Résidu}\\
& & \mbox{(Fixe)} & & \mbox{(Aléatoire)}
\end{array}$$
A cause de cette variable d'erreur, les valeurs numériques de coefficients que nous obtenons grâce au
logiciel doivent être considérées comme des estimations des paramètres vrais inconnus
$\beta_1$, $\beta_0$ et $\sigma^2$. Pour bien les distinguer dans l'écriture, nous écrirons avec un
chapeau ces paramètres estimés : $\hat{\beta}_1$, $\hat{\beta}_0$ et $\hat{\sigma}^2$.
Nous ne savons pas prévoir les valeurs que prendra cette variable d'erreur $\epsilon$, mais nous
pouvons
poser sur elle une hypothèse de distribution. Pour modéliser la distribution de
l'erreur,
deux propriétés semblent désirables :
-
On s'attend à ce que notre modèle se trompe autant en surestimation (résidu positif) qu'en
sous-estimation (résidu négatif) : la distribution devrait donc être symétrique par
rapport à 0.
-
On s'attend à ce que les erreurs très larges (en valeur absolue) soient plus rares que les erreurs
petites : la distribution devrait donc être unimodale (densités fortes autour d'une
valeur centrale).
Un choix de distribution naturel montrant ces deux propriétés est la loi
normale. Une telle loi de distribution
dérive d'un mécanisme d'addition d'une multitude de variables inconnues additionnant leurs effets de
manière indépendante. Elle est donc assez appropriée pour modéliser ce qu'on appelle de l'erreur,
c'est-à-dire l'impact perturbateur de la mesure engendré par un grand nombre de variables parasites
inconnues. La loi normale a cependant une propriété qui n'en fait pas toujours le meilleur choix pour
modéliser l'erreur : elle est définie sur toute la droite réelle $[-\infty;+\infty]$. Si la mesure
étudiée
est bornée (ce qui est le cas du prestige dans notre étude), elle sera (au mieux) une approximation.
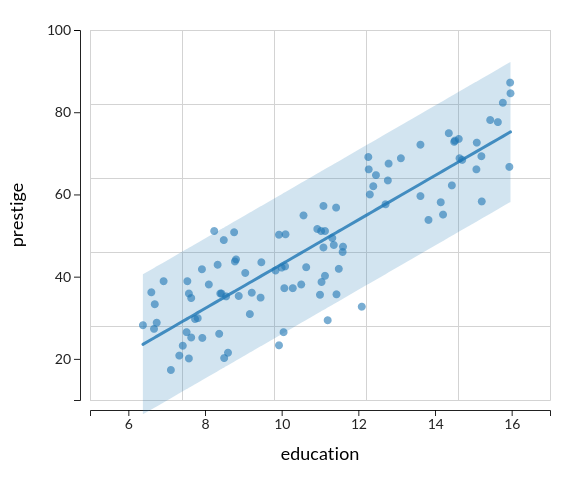
Dans l'onglet Graphiques, activez l'option d'affichage « Intervalle de prévision ». Cette
option permet de faire apparaître l'intervalle dans lequel nous avons 95% de chances d'observer des
points professions.
Il faut comprendre de cette représentation qu'un certain intervalle d'incertitude est pris en compte
par le modèle, sur la présence des points autour de la droite. Cet intervalle est exactement de même
largeur sur $Y$, pour toute valeur de $X$ qu'on considère, résultant ainsi en une « bande » de
variation. La largeur de cette bande est une représentation indirecte, probabiliste, de ce qu'on
appelle l'erreur du modèle.
Cette erreur est quantifiable sous la forme d'un écart-type dont la valeur ($\hat{\sigma}=
8.578318$)
peut-être trouvée en bas du tableau des paramètres. La largeur de l'intervalle de prédiction à 95%
est
environ de 4 fois cette erreur (34.31).
Dans les modèles gaussiens, on fait toujours l'hypothèse que la variance conditionnelle (ou erreur
conditionnelle) est constante, quelle que soit la valeur de $X$ qu'on considère, d'où l'allure en
bande de hauteur constante de l'intervalle de prévision. C'est ce qu'on appelle l'hypothèse
d'homogénéité de la
variance. En l'absence de bornes de la variable dépendante, cette hypothèse a du sens :
elle affirme que l'erreur manifeste son effet avec la même amplitude pour toute valeur du prédicteur
$X$. Dans d'autres contextes (notamment en présence de bornes), nous ferons des hypothèses
différentes.
Si nous choisissons un modèle unimodal et symétrique de distribution de l'erreur, on comprend que la
prévision $\hat{Y}$ prend la signification statistique d'une moyenne (ou espérance) conditionnelle :
c'est la moyenne de toutes les valeurs de $Y$ possibles pour un $X$ fixé. Si la droite de régression est
un ensemble de moyennes d'une infinité de distributions normales de même variance, on peut l'écrire sous
la forme qui fait mieux apparaître ce statut d'espérance :
$$E(Y|X=x)=\beta_{0}+\beta_{1}x$$
Nous allons appeler modèle structural de l'espérance la partie à droite de cette
équation. Ici la structure supposée est linéaire mais d'autres choix sont possibles (voir fiche suivante). On
appelle modèle de régression tout modèle structural sur une espérance conditionnelle,
qui appuie cette structure sur des variables explicatives (la durée de la scolarité par exemple).
Si on réunit les deux étages, structural et distributionnel, du modèle linéaire, il peut être écrit en
une seule expression synthétique :
$$Y|X\sim N(\beta_{0}+\beta_{1}X,\sigma^{2})$$
Cette écriture permet de rendre explicite que notre modèle contient à la fois une hypothèse sur la
forme du lien et sur la distribution de l'erreur. Pour estimer les
paramètres inconnus du modèle, on leur donne les valeurs numériques qui donnent aux données une
probabilité maximale selon la loi normale correspondante : c'est ce qu'on appelle estimer par
maximisation de la vraisemblance.
De façon intéressante, quand on fait cela, on s'aperçoit qu'on obtient exactement les mêmes estimations
de
paramètres de pente et d'intercept que si l'on cherche à minimiser la déviance. Mais l'avantage d'une
approche probabiliste est que nous allons pouvoir :
-
Juger de la qualité du modèle : on dira qu'un modèle est bon s'il nous annonce les données
observées comme très probables d'après lui. C'est ce qu'on appelle la vraisemblance
du
modèle.
-
prendre des décisions sur l'ampleur des coefficients, notamment pour tester qu'ils ne sont pas
le
pur produit d'une erreur d'échantillonnage.
Test de significativité des coefficients de régression
Une fois le paramètre de régression estimé, on se pose la question : que se passerait-il si nous recommencions
plusieurs fois la même étude, en interrogeant des panels
indépendants de personnes à chaque fois, et retestions ce modèle de nombreuses fois ? Les données
obtenues ne seraient pas à chaque fois les mêmes et
par conséquent notre estimation du paramètre $\beta_1$ changerait à chaque
fois. Cependant, elle
ne varierait pas n'importe comment : on peut montrer que, si la relation linéaire existe, et que la
distribution des données autour de la droite est bien normale, alors l'ensemble des valeurs possibles de
$\hat{\beta}_1$ suivront aussi une loi normale centrée sur la valeur vraie $\beta_1$ :
$$\hat{\beta}_1\sim N(\beta_1,\sigma_{\beta_1}^2)$$
On peut montrer qu'une estimation sans biais de la variance de cette loi normale de coefficient est :
$$\hat{\sigma}_{\beta_1}^2=\frac{\hat{\sigma}^2}{(N-1)s_{X}^2}$$
ou $\hat{\sigma}^2$ est la variance d'erreur de la régression et $s_{X}^2$ est la variance de la
variable
explicative $X$ (le nombre d'année d'études).
Exactement comme un test gaussien sur une moyenne, on peut donc former la
statistique de décision de Student qui intègre cette estimation de la variance inconnue
$\hat{\sigma}_{\beta_1}^2$ sous la forme :
$$T=\frac{\hat{\beta}_1 - \beta_1}{\hat{\sigma}_{\beta_1}}\sim t(N-p)$$
ou $p$ est le nombre de coefficients de régression (c'est-à-dire sans compter la variance).
Cela permet de tester le fait que notre coefficient de régression est significatif, c'est-à-dire
suffisamment grand pour qu'on ne puisse pas penser que la valeur vraie est 0 dans la population. Pour
mettre à l'épreuve l'hypothèse $\beta_1=0$, on la pose d'abord comme vraie et on regarde si la valeur
calculée de :
$$T=\frac{\hat{\beta}_1 - 0}{\hat{\sigma}_{\beta_1}}=\frac{\hat{\beta}_1}{\hat{\sigma}_{\beta_1}}$$
apparaît dans les valeurs probables d'une loi de Student $t(N-p)$, ou au contraire dans ses valeurs
extrêmes. Dans ce dernier cas, on jugera le coefficient estimé suffisamment grand pour rejeter
l'hypothèse
qu'il soit nul dans la population.
Exemple numérique
Dans l'étude de la relation Prestige-Instruction, nous avons estimé le coefficient principal à
$\hat{\beta}_1=5.3884$ et l'erreur standard de la régression à $\hat{\sigma}=8.578318$. Le nombre total
d'observations ($N=98$) et l'écart-type du nombre d'année d'études ($s_X=2.7489$) sont facilement
obtenus
dans l'interface en cliquant sur cette variable dans la liste principale. On a par ailleurs $p=2$
coefficients de régression estimés. L'écart-type de la distribution des estimations $\hat{\beta}_1$ est
donc estimé par :
$$\hat{\sigma}_{\beta_1}=\sqrt{\frac{\hat{\sigma}^2}{(N-1)s_{X}^2}}=\sqrt{\frac{8.578318^2}{(98-1)\times
2.7489^2}}=0.3168$$
On trouve cette valeur directement calculée par l'interface dans la colonne « Erreur-type » du tableau
des
paramètres.
Pour cette valeur d'erreur-type, le $t$ de Student testant l'égalité du coefficient à 0 vaut :
$$t=\frac{5.3884}{0.3168}\approx 17 (p < 0.000)$$ et la probabilité d'observer une telle valeur
d'estimation sous l'hypothèse d'une valeur vraie $\beta_1=0$ est... quasiment nulle (arrondie à 0 dans
l'interface).
Conclusion : le coefficient de la régression est significativement différent de 0 et, sous réserve
que
l'hypothèse de linéarité soit correcte, on peut donc conclure à une relation positive et
significative
entre niveau d'instruction et prestige social perçu des professions.
Exercice d'application
Atelier 4 : explication du prestige des professions par le niveau de revenu
Pour la même étude, nous pourrions aussi bien faire l'hypothèse que ce qui rend prestigieuse une
profession
est plutôt le niveau de revenu que le nombre d'années d'études.
-
A partir du même jeu de données, examinez le lien entre le prestige des professions et le niveau de
revenu moyen (Income) de la profession.
-
Quelles valeurs trouvez-vous pour $\hat{\beta}_0$, $\hat{\beta}_1$ et $\hat{\sigma}$ ?
-
Examiner l'allure graphique de la relation. Affichez l'intervalle de prévision. Un modèle linéaire
d'erreur constante vous paraît-il raisonnable ? Affichez un lissage des données pour appuyer votre
commentaire.
-
Quelle fonction mathématique connaissez-vous qui serait plus appropriée qu'une droite pour modéliser
cette relation ?
-
Retestez le modèle avec pour variable explicative logIncome et examinez l'allure du lissage.
Qu'en pensez-vous ?
-
Quelle conclusion tirez-vous du test de normalité ?
Nous avons supposé une relation de proportionnalité entre éducation et prestige : cette relation est-elle exacte ? D'après la feuille de résultats, le calculateur a estimé cette relation par l'équation de droite : $$Y=-10.8409+5.3884X$$ Mais deux points du graphique ont exactement même abscisse $x=9.93$, pour deux ordonnées différentes : $y_{1}=23.3$ et $y_{2}=50.2$ (repérez-les dans l'onglet Graphiques). Que peut donc représenter leur commune valeur modèle $\hat{y}=-10.8409+(5.3884\times9.93)=42.66591$, lue sur la droite ?
Nous comprenons à travers cet exemple qu'un modèle mathématique de la forme $Y=\beta_{0}+\beta_{1}X$ se trompe nécessairement sur des données imparfaites. Pour une valeur $X=x$ fixée, nous pouvons avoir $Y=y_{1},y_{2},...$. On appelle résidu de l'observation $i$ ($i=1,...,N$) la valeur d'erreur : $$e_{i}=y_{i}-(\beta_{0}+\beta_{1}x_{i}).$$ Pour bien distinguer ce que l'on observe de ce que prévoit le modèle, on note $\hat{Y}$ la prévision faite par le modèle. Données empiriques et prévision du modèle sont réunies par la relation : $$\begin{array}{ccccc} Y & = & \hat{Y} & + & \epsilon\\ & = & (\beta_{0}+\beta_{1}X) & + & \epsilon\\ \mbox{Score} & = & \mbox{Prévision} & + & \mbox{Résidu}\\ & & \mbox{(Fixe)} & & \mbox{(Aléatoire)} \end{array}$$
A cause de cette variable d'erreur, les valeurs numériques de coefficients que nous obtenons grâce au logiciel doivent être considérées comme des estimations des paramètres vrais inconnus $\beta_1$, $\beta_0$ et $\sigma^2$. Pour bien les distinguer dans l'écriture, nous écrirons avec un chapeau ces paramètres estimés : $\hat{\beta}_1$, $\hat{\beta}_0$ et $\hat{\sigma}^2$.
Nous ne savons pas prévoir les valeurs que prendra cette variable d'erreur $\epsilon$, mais nous pouvons poser sur elle une hypothèse de distribution. Pour modéliser la distribution de l'erreur, deux propriétés semblent désirables :
- On s'attend à ce que notre modèle se trompe autant en surestimation (résidu positif) qu'en sous-estimation (résidu négatif) : la distribution devrait donc être symétrique par rapport à 0.
- On s'attend à ce que les erreurs très larges (en valeur absolue) soient plus rares que les erreurs petites : la distribution devrait donc être unimodale (densités fortes autour d'une valeur centrale).
Un choix de distribution naturel montrant ces deux propriétés est la loi normale. Une telle loi de distribution dérive d'un mécanisme d'addition d'une multitude de variables inconnues additionnant leurs effets de manière indépendante. Elle est donc assez appropriée pour modéliser ce qu'on appelle de l'erreur, c'est-à-dire l'impact perturbateur de la mesure engendré par un grand nombre de variables parasites inconnues. La loi normale a cependant une propriété qui n'en fait pas toujours le meilleur choix pour modéliser l'erreur : elle est définie sur toute la droite réelle $[-\infty;+\infty]$. Si la mesure étudiée est bornée (ce qui est le cas du prestige dans notre étude), elle sera (au mieux) une approximation.

Dans l'onglet Graphiques, activez l'option d'affichage « Intervalle de prévision ». Cette option permet de faire apparaître l'intervalle dans lequel nous avons 95% de chances d'observer des points professions.
Il faut comprendre de cette représentation qu'un certain intervalle d'incertitude est pris en compte par le modèle, sur la présence des points autour de la droite. Cet intervalle est exactement de même largeur sur $Y$, pour toute valeur de $X$ qu'on considère, résultant ainsi en une « bande » de variation. La largeur de cette bande est une représentation indirecte, probabiliste, de ce qu'on appelle l'erreur du modèle.
Cette erreur est quantifiable sous la forme d'un écart-type dont la valeur ($\hat{\sigma}= 8.578318$) peut-être trouvée en bas du tableau des paramètres. La largeur de l'intervalle de prédiction à 95% est environ de 4 fois cette erreur (34.31).
Dans les modèles gaussiens, on fait toujours l'hypothèse que la variance conditionnelle (ou erreur conditionnelle) est constante, quelle que soit la valeur de $X$ qu'on considère, d'où l'allure en bande de hauteur constante de l'intervalle de prévision. C'est ce qu'on appelle l'hypothèse d'homogénéité de la variance. En l'absence de bornes de la variable dépendante, cette hypothèse a du sens : elle affirme que l'erreur manifeste son effet avec la même amplitude pour toute valeur du prédicteur $X$. Dans d'autres contextes (notamment en présence de bornes), nous ferons des hypothèses différentes.
Si nous choisissons un modèle unimodal et symétrique de distribution de l'erreur, on comprend que la prévision $\hat{Y}$ prend la signification statistique d'une moyenne (ou espérance) conditionnelle : c'est la moyenne de toutes les valeurs de $Y$ possibles pour un $X$ fixé. Si la droite de régression est un ensemble de moyennes d'une infinité de distributions normales de même variance, on peut l'écrire sous la forme qui fait mieux apparaître ce statut d'espérance : $$E(Y|X=x)=\beta_{0}+\beta_{1}x$$ Nous allons appeler modèle structural de l'espérance la partie à droite de cette équation. Ici la structure supposée est linéaire mais d'autres choix sont possibles (voir fiche suivante). On appelle modèle de régression tout modèle structural sur une espérance conditionnelle, qui appuie cette structure sur des variables explicatives (la durée de la scolarité par exemple).
Si on réunit les deux étages, structural et distributionnel, du modèle linéaire, il peut être écrit en une seule expression synthétique : $$Y|X\sim N(\beta_{0}+\beta_{1}X,\sigma^{2})$$ Cette écriture permet de rendre explicite que notre modèle contient à la fois une hypothèse sur la forme du lien et sur la distribution de l'erreur. Pour estimer les paramètres inconnus du modèle, on leur donne les valeurs numériques qui donnent aux données une probabilité maximale selon la loi normale correspondante : c'est ce qu'on appelle estimer par maximisation de la vraisemblance.
De façon intéressante, quand on fait cela, on s'aperçoit qu'on obtient exactement les mêmes estimations de paramètres de pente et d'intercept que si l'on cherche à minimiser la déviance. Mais l'avantage d'une approche probabiliste est que nous allons pouvoir :
- Juger de la qualité du modèle : on dira qu'un modèle est bon s'il nous annonce les données observées comme très probables d'après lui. C'est ce qu'on appelle la vraisemblance du modèle.
- prendre des décisions sur l'ampleur des coefficients, notamment pour tester qu'ils ne sont pas le pur produit d'une erreur d'échantillonnage.
Une fois le paramètre de régression estimé, on se pose la question : que se passerait-il si nous recommencions plusieurs fois la même étude, en interrogeant des panels indépendants de personnes à chaque fois, et retestions ce modèle de nombreuses fois ? Les données obtenues ne seraient pas à chaque fois les mêmes et par conséquent notre estimation du paramètre $\beta_1$ changerait à chaque fois. Cependant, elle ne varierait pas n'importe comment : on peut montrer que, si la relation linéaire existe, et que la distribution des données autour de la droite est bien normale, alors l'ensemble des valeurs possibles de $\hat{\beta}_1$ suivront aussi une loi normale centrée sur la valeur vraie $\beta_1$ : $$\hat{\beta}_1\sim N(\beta_1,\sigma_{\beta_1}^2)$$ On peut montrer qu'une estimation sans biais de la variance de cette loi normale de coefficient est : $$\hat{\sigma}_{\beta_1}^2=\frac{\hat{\sigma}^2}{(N-1)s_{X}^2}$$ ou $\hat{\sigma}^2$ est la variance d'erreur de la régression et $s_{X}^2$ est la variance de la variable explicative $X$ (le nombre d'année d'études).
Exactement comme un test gaussien sur une moyenne, on peut donc former la statistique de décision de Student qui intègre cette estimation de la variance inconnue $\hat{\sigma}_{\beta_1}^2$ sous la forme : $$T=\frac{\hat{\beta}_1 - \beta_1}{\hat{\sigma}_{\beta_1}}\sim t(N-p)$$ ou $p$ est le nombre de coefficients de régression (c'est-à-dire sans compter la variance).
Cela permet de tester le fait que notre coefficient de régression est significatif, c'est-à-dire suffisamment grand pour qu'on ne puisse pas penser que la valeur vraie est 0 dans la population. Pour mettre à l'épreuve l'hypothèse $\beta_1=0$, on la pose d'abord comme vraie et on regarde si la valeur calculée de : $$T=\frac{\hat{\beta}_1 - 0}{\hat{\sigma}_{\beta_1}}=\frac{\hat{\beta}_1}{\hat{\sigma}_{\beta_1}}$$ apparaît dans les valeurs probables d'une loi de Student $t(N-p)$, ou au contraire dans ses valeurs extrêmes. Dans ce dernier cas, on jugera le coefficient estimé suffisamment grand pour rejeter l'hypothèse qu'il soit nul dans la population.
Exemple numérique
Dans l'étude de la relation Prestige-Instruction, nous avons estimé le coefficient principal à $\hat{\beta}_1=5.3884$ et l'erreur standard de la régression à $\hat{\sigma}=8.578318$. Le nombre total d'observations ($N=98$) et l'écart-type du nombre d'année d'études ($s_X=2.7489$) sont facilement obtenus dans l'interface en cliquant sur cette variable dans la liste principale. On a par ailleurs $p=2$ coefficients de régression estimés. L'écart-type de la distribution des estimations $\hat{\beta}_1$ est donc estimé par : $$\hat{\sigma}_{\beta_1}=\sqrt{\frac{\hat{\sigma}^2}{(N-1)s_{X}^2}}=\sqrt{\frac{8.578318^2}{(98-1)\times 2.7489^2}}=0.3168$$ On trouve cette valeur directement calculée par l'interface dans la colonne « Erreur-type » du tableau des paramètres.
Pour cette valeur d'erreur-type, le $t$ de Student testant l'égalité du coefficient à 0 vaut : $$t=\frac{5.3884}{0.3168}\approx 17 (p < 0.000)$$ et la probabilité d'observer une telle valeur d'estimation sous l'hypothèse d'une valeur vraie $\beta_1=0$ est... quasiment nulle (arrondie à 0 dans l'interface).
Conclusion : le coefficient de la régression est significativement différent de 0 et, sous réserve que l'hypothèse de linéarité soit correcte, on peut donc conclure à une relation positive et significative entre niveau d'instruction et prestige social perçu des professions.
Atelier 4 : explication du prestige des professions par le niveau de revenu
Pour la même étude, nous pourrions aussi bien faire l'hypothèse que ce qui rend prestigieuse une profession est plutôt le niveau de revenu que le nombre d'années d'études.- A partir du même jeu de données, examinez le lien entre le prestige des professions et le niveau de revenu moyen (Income) de la profession.
- Quelles valeurs trouvez-vous pour $\hat{\beta}_0$, $\hat{\beta}_1$ et $\hat{\sigma}$ ?
- Examiner l'allure graphique de la relation. Affichez l'intervalle de prévision. Un modèle linéaire d'erreur constante vous paraît-il raisonnable ? Affichez un lissage des données pour appuyer votre commentaire.
- Quelle fonction mathématique connaissez-vous qui serait plus appropriée qu'une droite pour modéliser cette relation ?
- Retestez le modèle avec pour variable explicative logIncome et examinez l'allure du lissage. Qu'en pensez-vous ?
- Quelle conclusion tirez-vous du test de normalité ?