Qualités et comparaisons des modèles

Le modèle de régression linéaire peut facilement être généralisé pour inclure plusieurs prédicteurs conjoints, sous la forme : $$\hat{Y}=\beta_1 X_1 + \beta_2 X_2$$ Le pouvoir explicatif supplémentaire apporté par le prédicteur supplémentaire $X_2$ peut être testé en testant la réduction de la déviance qu'il apporte. C'est ce que l'on voit dans l'atelier suivant.

Atelier 1 : explication conjointe du prestige par l'instruction et le revenu

Les sections qui suivent détaillent la signification de l'ensemble des résultats numériques qui apparaissent dans l'interface.

Dans la démarche de modélisation, on procède toujours en deux étapes :

• On commence toujours par identifier le meilleur modèle dont on dispose, avec les variables explicatives qu'on a envisagées.
• Puis, dans un second temps, on examine les coefficients au sein du meilleur modèle, pour détecter et interpréter les effets intéressants. Il s'agit de détecter les effets de taille suffisante pour qu'on ne les assimile pas à de la pure erreur d'échantillonnage.

Lire des résultats de tests sur coefficients au sein d'un modèle erroné, c'est s'exposer à interpréter des effets illusoires ou à en écarter qui étaient intéressants. On examine dans cette partie les différents indices permettant de réaliser cette sélection de modèle.

Analyse de la déviance

Une première mesure naturelle de (mauvaise) qualité du modèle est sa déviance. Par exemple, notre modèle explicatif $M_1$ impliquant le niveau d'études a une déviance de $D_1=7064.4045$. Si on le compare au modèle constant, qui ne suppose aucun lien, on trouve $D_0=28346.8756$, soit une déviance 4 fois plus grande. La même information peut être présentée de façon un peu différente.

Le modèle $M_0$ est un modèle sans structure. Il représente en réalité un résumé des données par leur seule moyenne. Sa déviance est comme une mesure de ce qu'on pourrait appeler la variabilité totale des données. On peut donc se demander comment un modèle plus structuré parvient à rendre compte de la dispersion totale des données. La quantité : $$R_1=D_0-D_1=28346.8756-7064.4045=21282.47$$ mesure ce que nous appeler la réduction de la déviance. Elle nous apprend qu'en incluant le facteur explicatif Niveau d'instruction, nous réduisons l'erreur sur l'explication des données de 21282.47 points de déviance.

Il n'existe pas de test permettant de juger qu'une déviance est petite ou grande. Par contre il existe un test comparatif permettant de juger qu'une déviance est significativement plus petite qu'une autre : c'est le test de Fisher sur la réduction de la déviance. Nous ne détaillons pas ici le principe théorique du test (voir le manuel de cours, chapitre 9, p. 286, ou cette section) mais simplement sa mise en oeuvre : nous dirons que la réduction de la déviance est significative si la valeur $p$ du test de Fisher apparaissant dans la colonne 'F' du tableau d'analyse de la déviance est inférieure à un certain seuil de décision (par exemple $\alpha=0.05$).

Par exemple, les analyses précédentes sont résumées dans la table d'analyse de la déviance :

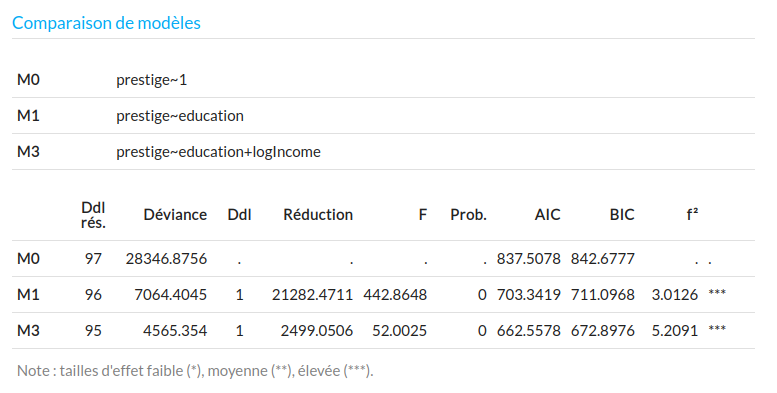
On voit que dans la séquence des trois modèles, l'introduction de la variable explicative Education (en passant de M0 à M1) a amené une réduction de déviance significative ($F=442.86$, $p < 0.000$) de 21282 points de déviance dans l'explication du prestige. Cette variable joue donc un rôle significatif dans son explication. Mais l'introduction du log-revenu amène aussi une réduction significative ($F=52$, $p < 0.000$) de 2500 points de déviance, ce qui en fait une variable explicative importante aussi (même si la réduction de déviance est moindre).

Dans cette situation, le meilleur modèle est $M_2$ : la perception sociale du prestige des professions est conjointement déterminée par le niveau d'instruction requis et par le revenu moyen associé. Si l'on supprime l'une ou l'autre de ces deux variables, on se prive d'une partie substantielle de l'explication.

L'approche par analyse de la réduction de la déviance est très flexible mais comporte une subtilité. Le $F$ de Fisher est calculé de façon incrémentielle : il mesure l'apport spécifique d'une variable, en termes d'explication de la VD, quand on l'ajoute à d'autres prédicteurs déjà entrés. Or, il existe plusieurs manières de faire cela et toutes ne donnent pas nécessairement le même $F$ ! Pour vous en convaincre, testez la séquence de modèles qui fait entrer d'abord le log-revenu, puis ensuite ajoute l'instruction. Les $F$ de Fisher mesurant l'impact des deux prédicteurs ne sont plus les mêmes : la réduction de la déviance est cette fois-ci plus importante pour le LogRevenu que pour l'Instruction.

Le problème est lié à la corrélation entre les prédicteurs : les gens qui ont des revenus élevés ont en moyenne un cursus plus long. Si deux variables explicatives sont corrélées, alors il n'existe pas qu'une seule manière d'expliquer la VD en les combinant. Chacune d'entre elle peut expliquer une partie commune de déviance et l'ordre dans lequel on les teste a alors de l'importance : la première entrée explique tout ce qu'elle peut, ne laissant à l'autre que la part qu'elle peut expliquer dans ce qui reste. Ce n'est pas un problème majeur si l'on cherche seulement à argumenter le fait que les deux variables, Instruction et LogRevenu, contribuent à l'explication de la perception sociale du prestige des professions. Par contre, c'est un problème si l'on cherche absolument à quantifier les pouvoirs explicatifs de l'une et de l'autre, pour affirmer par exemple que l'Instruction serait plus déterminante que le Revenu dans l'explication du prestige.

Il n'y a pas de solution totalement satisfaisante à ce problème. Trois modes de calcul de la réduction de la déviance (ou sommes de carrés) sont utilisés en pratique :

• l'approche séquentielle (somme de carrés de type I) : on entre un facteur après l'autre, et on observe l'évolution de la réduction de la déviance. Dans cette approche, on doit décider de l'ordre dans lequel on entre les variables, puisqu'on sait qu'on n'obtiendra pas le même résultat selon l'ordre choisi. Un principe simple est de toujours entrer en premier les variables qui porte moins d'intérêt théorique : si les variables réellement intéressantes (entrées en dernier) continuent d'avoir un pouvoir explicatif significatif malgré le privilège accordé aux variables de contrôle, alors on est d'autant plus convaincu de l'importance des variables théoriquement intéressantes.

  Par exemple ici, imaginons que nous cherchions à étayer le fait que le niveau d'étude joue un rôle dans la perception sociale du prestige, et que ce n'est pas simplement une affaire de salaire : nous donnerons le maximum de place au revenu, en l'entrant en premier dans le modèle, pour observer si le niveau d'étude, entré en second, a bien un pouvoir explicatif significatif. Nous serons alors certains que le pouvoir explicatif mesuré pour le niveau d'étude ne doit rien à sa corrélation avec le revenu.

• l'approche hiérarchique (somme des carrés de type II) : on mesure l'importance d'un prédicteur en comparant le modèle qui inclut toutes les autres variables (et leurs éventuelles interactions) avec le modèle qui ajoute en plus ce prédicteur. Cela oblige à faire une comparaison de modèle pour chaque prédicteur. Par exemple ici : on compare M1 avec M3 pour juger de la réduction de la déviance apportée par le LogRevenu (voir table d'analyse de la déviance ci-dessus) : la réduction de la déviance de type II imputable à l'introduction du LogRevenu dans le modèle, tout autre facteur pris en compte, est de $R_{13}=2499.05$. Et on compare M2 avec M3 pour juger de la contribution propre du niveau d'instruction :
  

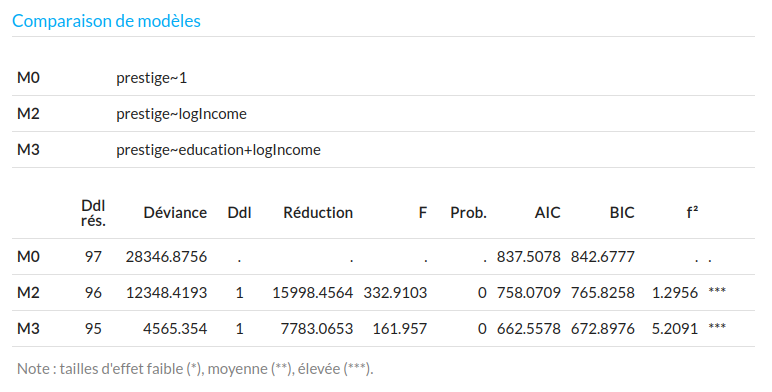
  La réduction de la déviance de type II, imputable au niveau d'instruction, le LogRevenu pris en compte, est de $R_{23}=7783.06$. On peut donc dire que, dans l'explication du prestige des professions, la part explicative propre du niveau d'étude est au moins 3 fois plus importante que celle du revenu.

• l'approche par calcul de la part unique (somme des carrés de type III) : on compare un modèle qui inclut tous les effets (principaux et d'interaction, même si les interactions incluent le facteur testé) avec le modèle qui inclut en plus le facteur testé, en effet principal. Naturellement, si aucun terme d'ordre supérieur (en particulier des interactions) n'est présent dans le modèle, cette approche donnera les mêmes résultats que l'approche précédente (ce qui est notre cas ici). Dans les autres cas, les réductions de déviance apportée par l'effet principal de la variable ont des valeurs différentes. Par exemple, pour tester les effets dans un modèle de la forme : $$M_1:\ \hat{Y}\sim X_1 + X_2 + X1.X2$$ on le comparera successivement aux modèles : $$M_2:\ \hat{Y}\sim X_2 + X1.X2$$ $$M_3:\ \hat{Y}\sim X_1 + X1.X2$$

  La comparaison $M_1/M_2$ permet de quantifier la réduction de la déviance apportée spécifiquement par l'effet principal $X_1$, et la comparaison $M_1/M_3$ permet de quantifier la réduction de la déviance apportée spécifiquement par l'effet principal $X_2$. Mais cette approche est assez contestée car elle oblige à construire des modèles ($M_2$ et $M_3$ ici) qui intègrent des effets d'interaction sans inclure des effets principaux associés, ce qui n'a pas toujours du sens (on parle de violation du principe de marginalité).

Les approches de calcul de la réduction de la déviance de type II et III sont assez artificielles, et représentent des mesures conservatrices pour tenter de neutraliser l'impact de la corrélation des prédicteurs sur l'évaluation séparée de leurs poids explicatifs. Il est important de comprendre que ces procédures (en dépit du fait qu'elles sont parfois calculées par défaut par certains logiciels) ne sont en aucun cas nécessaires s'il n'y a pas d'enjeu à quantifier les poids explicatifs des variables causales. Dans ce cours, on privilégiera toujours l'approche séquentielle, qui demande en outre à réfléchir au statut de ses variables (principale ou contrôlée).

Le coefficient de détermination

Cette réduction de déviance peut aussi être présentée comme un gain explicatif sur la dispersion totale des données $D_0=28346.8756$. On peut donc dire que $M_1$ explique : $$R^2=\frac{D_0-D_1}{D_0}=\frac{21282.47}{28346.8756}=0.7508$$ c'est-à-dire 75% de la déviance nulle. Le coefficient noté $R^2$ est appelé coefficient de détermination : il mesure le pourcentage de la déviance totale expliqué par l'introduction du facteur explicatif Niveau d'études. Cette notation se justifie de ce qu'il est exactement égal au carré du coefficient de corrélation entre les deux variables Prestige et Instruction.

Mesures pénalisées pour le nombre de paramètres

Une mesure (inversement) proportionnelle à la déviance est la vraisemblance (probabilité des données d'après le modèle), transformée en logarithme : c'est ce qu'on appelle la log-vraisemblance. Un bon modèle doit avoir une log-vraisemblance aussi élevée que possible.

Cependant, il est assez facile d'augmenter la log-vraisemblance ou le $R^2$ (ou de diminuer la déviance) d'un modèle en ajoutant de nombreuses variables explicatives (ce qui ajoute de nombreux paramètres $\beta$ à estimer). On cherche en général dans la modélisation une forme de parcimonie du modèle, c'est-à-dire une forme de compromis entre la qualité (logvraisemblance) et la simplicité (petit nombre de paramètres) : un modèle ayant à peu près le même pouvoir explicatif mais avec moins de paramètres sera toujours préférable. Pour le dire autrement : il serait très facile d'avoir des modèles parfaitement ajustés au données en ayant autant de paramètres que de données, mais les résultats ne se généraliseraient pas bien à d'autres jeux de données du même type, et cela n'aurait donc pas beaucoup d'intérêt scientifique. La notion de simplicité ou de parcimonie du modèle entre donc en ligne de compte dans le choix d'un bon modèle.

C'est ce que réalisent les mesures de $R^2$ ajusté, $AIC$ (Akaike Information Criterion) et $BIC$ (Bayesian Information Criterion). Parmi eux, nous utiliserons préférentiellement le $BIC$, qui a une interprétation très simple : le modèle qui a le plus petit $BIC$ est le plus probablement vrai (attention au sens inversé de l'interprétation). Il va nous permettre de déployer une démarche de comparaison et de sélection du modèle le plus probable pour un jeu de données.

La sélection de modèle par le $BIC$ est certainement la plus simple qui existe : sur un ensemble de modèles concurrents testés, on garde celui qui a le plus petit $BIC$. Le $BIC$ mesure la qualité globale d'un modèle, et n'est donc pas une statistique incrémentielle, contrairement au $F$ de Fisher : sa valeur ne change pas selon l'ordre d'entrée des variables dans la séquence des modèles. La sélection automatique par $BIC$ des variables les plus explicatives est obtenue dans R2STATS en définissant un modèle incluant toutes les variables explicatives dont on dispose, et en basculant du mode Manuel (en bas à droite de l'interface) en mode Auto : on clique sur Estimer et le logiciel essaie tous les sous-modèles possibles de M3. Il rapporte en résultats celui qui a le plus petit $BIC$ (et qui est donc le plus probablement vrai). En entrant M3 dans l'interface (qui inclut à la fois le LogRevenu et le niveau d'études), on voit que la sélection automatique retient les deux variables comme prédicteurs importants.

Le modèle de régression linéaire intègre 4 hypothèses :

1. la linéarité de la relation,
2. la normalité de la distribution des résidus,
3. l'homogénéité de la variance d'erreur,
4. l'indépendance des résidus.

Les hypothèses de linéarité, de normalité et d'homogénéité de la variance ne sont pas triviales. Dans chaque situation où nous utiliserons un modèle linéaire, nous prendrons soin de tester que l'allure générale de la relation peut raisonnablement être considérée comme linéaire, et que la distribution des points autour de la droite respecte bien le schéma de variance homogène attendu par un modèle de loi normale de variance constante.

Linéarité

Un test de linéarité est possible dans le cas assez particulier où les valeurs du prédicteur $X$ sont associées à plusieurs valeurs de $Y$. Le prédicteur peut alors être artificiellement manipulé comme un facteur de groupe, à l'intérieur duquel on calcule des moyennes conditionnelles (non contraintes à l'alignement) de $Y$. On peut alors comparer la déviance d'un tel modèle (qui n'est autre qu'un modèle d'ANOVA) à la déviance de la régression (qui impose l'alignement des moyennes) pour montrer que la réduction de la déviance apportée par l'ANOVA n'est pas significative.

Comme il est rare de se retrouver dans la situation où l'on dispose d'un nombre suffisant de valeurs de $Y$ pour chaque valeur distincte de $X$, on préférera dans la plupart des cas utiliser l'option Lissage de R2STATS, en superposition avec la droite de régression, pour détecter d'éventuelles écarts systématiques à la linéarité. Sur la figure ci-dessous, on représente le modèle du prestige expliqué par le niveau d'instruction et le log-revenu, en superposant la droite de régression avec un lissage (une forme de régression élastique, sans contrainte de linéarité) : on peut constater que le lissage se confond pratiquement avec la droite.

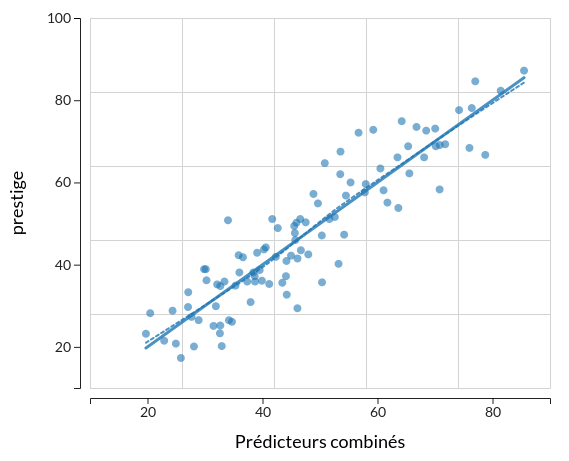
Normalité de la distribution des résidus

Nous revoyons succinctement dans cette partie le test de normalité $W$ de Shapiro-Wilk, présenté dans un précédent chapitre. Sa valeur est rapportée dans l'onglet Résultats à la rubrique « Test des conditions ». On lit $W=0.97903$ ($p < 0.1192$). La statistique W de Shapiro-Wilk est analogue à une corrélation (au carré) entre les résidus observés et les résidus tels qu'on devrait les observer s'ils étaient issus d'une loi normale. Elle varie donc entre 0 et 1. Plus cette valeur est grande (proche de 1), plus l'hypothèse de normalité paraît donc crédible.

On juge cependant de la taille de $W$ en calculant la probabilité d'obtenir une valeur plus faible sous hypothèse de normalité : plus cette probabilité est élevée, plus cela signifie que le $W$ est grand. Pour considérer que $W$ est grand, nous exigeons que sa valeur $p$ associée soit au moins égale à 0.10. On note que ce test s'interprète donc en sens inverse des tests d'effets usuels : plus la valeur $p$ est grande, plus nous jugeons crédible l'hypothèse de normalité. Cela se comprend assez bien si on garde à l'esprit que le test de normalité est un test d'ajustement : on cherche à argumenter que l'écart entre distribution réelle des résidus et loi normale n'est pas significatif.

Avec $W=0.97903$ et $p = 0.1192$, nous jugeons ici au seuil $\alpha=0.10$ que le $W$ est grand, et acceptons l'approximation par la loi normale.

Homogénéité de la variance d'erreur

Le propre de l'erreur est de n'avoir pas de caractère systématique, en particulier de n'avoir pas de relation avec le ou les prédicteurs. Il n'y a donc pas de raison d'observer plus d'erreur pour certaines valeurs de $X$ : on attend donc légitimement une variance de l'erreur qui soit de même amplitude pour toute valeur de $X$, c'est-à-dire graphiquement une distribution des points qui se maintient à l'intérieur d'une bande de largeur constante autour de la droite de régression. Attention cependant : ce raisonnement ne vaut que si la variable n'a pas de borne inférieure ou supérieure qui fait sentir son effet (seuil ou plafond), et réduirait mécaniquement la variance.

Tout comme pour le test de linéarité, si les différentes valeurs de $X$ sont associées à plusieurs valeurs de $Y$, il est possible de faire un test formel d'homogénéité de la variance en considérant $X$ comme un facteur. Cela suppose d'avoir suffisamment de valeurs de $Y$ dans ces groupes artificiels. Le plus souvent, on examine simplement le graphique de régression en activant l'option graphique Intervalle de prédiction dans R2STATS, pour constater que 95% de valeurs sont bien incluses dans la bande graphique qui apparaît.

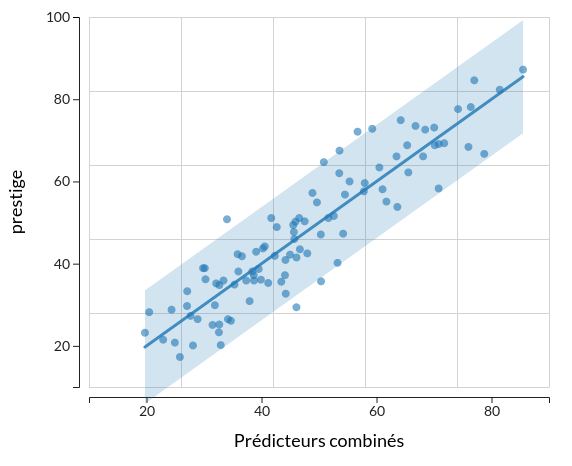
Indépendance des résidus

Les résidus, une fois rangés selon un quelconque critère (valeurs croissantes de $X$ ou dates de collecte, par exemple), ne doivent pas montrer de schéma systématique de corrélation sérielle : une augmentation ou une diminution progressive par exemple. Bien que des statistiques formelles puissent aider à le mesurer (test de Durbin-Watson, ou auto-corrélation pour des données temporelles), l'examen du graphique de régression suffit le plus souvent à le détecter. Dans la plupart des cas, cette auto-corrélation viendra indiquer qu'une ou plusieurs variables explicatives importantes sont absentes du modèle (le temps par exemple). Ce sera donc une incitation à réfléchir sur les variables indépendantes oubliées.

Prédicteurs de la réussite scolaire

Téléchargez et enregistrez sur votre disque le fichier DonneesScolaires.csv (merci à Alain Lieury de m'avoir communiqué ces données). Il contient les notes en français (variable « fran ») et en maths (variable « maths ») de $N=397$ élèves de collège et de lycée, de 9 à 17 ans. Cette étude vise à mettre en évidence l'importance de la maîtrise du vocabulaire dans la réussite scolaire, dans plusieurs disciplines. A côté des notes de français et de maths (que l'on va chercher à expliquer), quatre résultats à des tests langagiers spécialisés sont enregistrés, qui vont nous servir de variables explicatives : i) le vocabulaire en compréhension (quand on lit les mots, variable « VocComp »), ii) le vocabulaire en expression (quand on parle, variable « VocExpr »), iii) la maîtrise de la morphologie du français (variable « morpho ») et iv) la compréhension du sens des énoncés (variable « sens »).

1. Testez tour à tour et séparément chacun des 4 prédicteurs potentiels de la réussite en français, dans des modèles qu'on appellera M1, M2, M3 et M4. Rangez-les par ordre de qualité décroissante, en utilisant le $BIC$.
2. Trouvez un modèle parcimonieux permettant d'expliquer au mieux la note en français à partir d'un sous-ensemble suffisant de ces scores cognitifs, en commençant par les plus explicatifs. Les 4 prédicteurs sont-ils nécessaires ?
3. Strictement parlant, l'approche précédente est un peu heuristique. Il faudrait tester tous les sous-ensembles possibles de prédicteurs, et pas seulement ceux qu'on construit à partir d'un pré-rangement de qualité. Créez un modèle incluant les 4 prédicteurs dans R2STATS, et utilisez le mode automatique de détection de meilleur modèle pour une recherche exhaustive.
4. En fonction de vos résultats, nuancez les attentes des auteurs de l'étude quant à l'importance du vocabulaire.
5. Commentez le test de normalité du modèle final. Essayez de le commenter en examinant le graphique de régression de votre modèle final. Qu'observez-vous ?
6. Traitez les 3 points précédents de la même façon, en essayant de prédire la note en maths à partir des mêmes tests langagiers. La hiérarchie des prédicteurs est-elle la même ?

• expand_moreCorrection

  En procédant aux analyses, on constate que :

  • les prédicteurs potentiels, hiérarchisés par le $BIC$ apparaissent dans l'ordre de qualité décroissante : morpho, vocExpr, sens, vocComp.
  • quand on entre ces prédicteurs de façon cumulative les uns après les autres, dans un modèle de régression multiple de complexité croissante,, on constate que le modèle le plus probablement vrai est celui qui inclut les deux premières variables (morpho et vocExpr).
  • la condition de normalité est rejetée pour tous les modèles testés. Les notes de français sont comprises entre 0 et 100, et un effet plafond peut être responsable de cet échec de la normalité. En réalité un modèle de régression Beta serait plus approprié dans ce contexte.
  • De façon très intéressante, en procédant à la même analyse sur les notes en maths, on constate que la hiérarchie des prédicteurs est la même, ainsi que la sélection des variables suffisantes (morpho et vocExpr), indiquant que ces compétences cognitives sont des bases trasnversales de la réussite scolaire.