L'analyse de la variance
Notion de déviance
Modèles de groupes
L'approche par $T$ de Student est appropriée quand on souhaite comparer deux moyennes : on teste le fait que la différence des deux moyennes puisse être nulle dans les populations parentes. Dans cette partie, nous étudions un principe différent de comparaisons de moyennes, qui a l'avantage de pouvoir traiter la comparaison simultanée de plus de deux moyennes. Elle s'appuie sur la notion de modèle et d'erreur (ou de déviance) de modèle. Comme cette approche est valide également pour deux groupes, nous la présentons ci-après dans le cas de deux groupes, par simplicité, et sans perte de généralité.
Le test de l'égalité de deux moyennes peut être présenté comme la mise en concurrence de deux modèles : un modèle qui affirme l'égalité des moyennes (appelons-le $M_0$), et un modèle qui affirme leur différence (appelons-le $M_1$).
Dans ce qui suit, on va noter par $j=1,\ldots,J$ le numéro du groupe qu'on considère (dans cet exemple le nombre de groupes est $J=2$), et par $Y_j$ la variable dépendante (par exemple le QI) dans le groupe $j$.
Si l'on suppose que la variable dépendante suit une loi normale, ces deux modèles peuvent s'écrire de façon très analogue à ce que nous avons écrit pour les modèles binomiaux : $$\begin{aligned} M_{0}&:\ Y_{j}\sim N(\mu,\sigma^{2}) \\ M_{1}&:\ Y_{j}\sim N(\mu_{j},\sigma^{2}) \end{aligned} $$
La première expression signifie qu'on suppose que c'est exactement la même distribution normale dans les deux groupes, avec une unique moyenne $\mu$ et une unique variance $\sigma^2$. Si les scores ont la même distribution, c'est qu'il n'y a pas de différence entre les garçons et les filles du point de vue de cette performance, dans l'étude sur le QI et le genre.
La seconde expression signifie qu'on suppose que les deux populations sont caractérisées par deux distributions normales différentes, avec deux moyennes $\mu_1$ et $\mu_2$, mais une unique variance $\sigma^2$ (par hypothèse d'homogénéité des variances, déjà discutée). Si les scores ont une distribution différente, c'est qu'il y a bien une différence entre les garçons et les filles du point de vue de cette performance.
Les deux modèles annoncent donc une structure de moyenne différente sur les données. Les valeurs $\mu$, $\mu_1$ et $\mu_2$ sont évidemment inconnues dans l'une ou l'autre hypothèse, mais dans ce qui suit, on les estime au maximum de vraisemblance par les moyennes empiriques $\bar{Y}$ (moyenne générale de tous les scores observés), $\bar{Y}_1$ (moyenne observée dans le groupe 1), et $\bar{Y}_2$ (moyenne observée dans le groupe 2).
La question est alors de savoir quel modèle a le meilleur pouvoir descriptif pour un jeu de données. Nous sommes ici dans le cas le plus simple de ce qu'on appelle une approche par comparaison de modèles.
La déviance : une mesure de la divergence entre modèle et données
Dans ce qui suit, on numérote par $i$ ($i=1,...,n_j$) les $n_j$ sujets du groupe $j$, on numérote par $j$ les groupes expérimentaux ($j=1,\ldots,J$) et on note la variable de score pour un sujet $i$ dans le groupe $j$ par $Y_{ij}$.
Pour juger de la qualité du modèle $M_0$, nous allons calculer une quantité nommée déviance : $$D_{0}=\sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y}\right)^{2}$$ On peut voir cette mesure comme une mesure de distance entre les données observées $Y_{ij}$ et une certaine hypothèse de moyenne (ici unique $\mu$). Si les données sont effectivement massées autour d'un seul centre, cette quantité devrait être faible.
Mais s'il existe en réalité deux sous-groupes sous-jacents de scores et non un seul, cette quantité sera inutilement grande, à cause de la contrainte excessive d'un point central unique, et $M_1$ sera un modèle approprié. De façon analogue pour $M_1$, nous allons calculer : $$D_{1}=\sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y_j}\right)^{2}$$ Si la structure vraie est à deux groupes latents, on devrait avoir $D_1 < D_0$. Dans cette approche, toute la question de décider si deux moyennes inconnues sont différentes ou identiques revient donc à décider si la déviance est plus faible pour le modèle $M_1$ que pour $M_0$. Il est équivalent de décider si la réduction de la déviance : $$R_{01}=D_0-D_1=\sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y}\right)^{2}-\sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y_j}\right)^{2}$$ est faible.
Après un petit calcul, on montre que cette expression peut être réécrite sous la forme (voir Manuel de cours, chapitre 9) : $$R_{01}=\sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(\bar{Y_j}-\bar{Y}\right)^{2}=\sum_{j=1}^{J}n_j\left(\bar{Y_j}-\bar{Y}\right)^{2}$$
Il est habituel dans les manuels de réunir les trois quantités (déviance de $M_0$, déviance de $M_1$ et réduction de la déviance) en une seule expression sous la forme : $$\begin{array}{ccccc} D_{0} & = & R_{01} & + & D_{1}\\ \sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y}\right)^{2} & = & \sum_{j=1}^{J}n_{j}\left(\bar{Y_{j}}-\bar{Y}\right)^{2} & + & \sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y_{j}}\right)^{2} \end{array}$$
La déviance nulle $D_0$ est aussi appelée somme des carrés totale, $R_{01}$ est aussi appelée somme des carrés inter-groupe (car elle mesure strictement une dispersion des moyennes de groupe) et $D_1$ somme des carrés intra-groupe (car elle mesure la dispersion des scores individuels dans chaque groupe). Néanmoins ce vocabulaire est restreint aux modèles gaussiens car dans les autres distributions, la déviance ne prend pas la forme de sommes de carrés et on préférera donc dans ce cours parler de déviances.
Atelier : calcul de déviances
Le tableau ci-dessous contient les scores de coopération des sujets, dans les conditions Publique et Anonyme. Il contient également les valeurs prévues par les modèles $M_0$ (modèle constant ou nul) et le modèle $M_1$ (modèle de la différence inter-conditions). On note que les prévisions de scores réalisées par ces modèles sont simplement des moyennes : la moyenne générale dans le modèle qui ne distingue pas les groupes, et les moyennes de groupe dans le modèle de la différence inter-conditions.
Calculs des résidus
- Cliquez sur le bouton de téléchargement ci-dessous pour ouvrir le fichier dans un tableur (nous allons faire un peu de calcul).
- Calculez dans une cinquième colonne (Résidus M0) les résidus du modèle nul.
- Calculez dans la colonne suivante (Résidus M1) les résidus du modèle de la différence des conditions.
Calculs des déviances et réduction
La déviance est simplement la somme des carrés des résidus d'un modèle.
-
Calculez la déviance de M0, en bas de la colonne Résidus M0 :
=SOMME.CARRES(E2:E21). -
Faites de même pour M1, en bas de la colonne Résidus M1 :
=SOMME.CARRES(F2:F21). - Calculez enfin la différence des deux déviances dans une case adjacente.
Le fichier final obtenu peut être téléchargé au format OpenOffice ou EXCEL.
La valeur $R_{10}=1095.2$ représente la réduction de la déviance que l'on obtient quand on passe d'un modèle constant à un modèle à deux niveaux de groupe. Nous dirons que $M_1$ est un meilleur modèle si nous pouvons montrer que cette réduction est significative. Pour juger qu'elle l'est, nous avons besoin d'un modèle de distribution sur cette réduction, quand les moyennes sont en réalité égales dans les populations parentes.
Inférence
La réduction de la déviance, divisée par la variance vraie des données, a une distribution connue : $$\frac{R_{01}}{\sigma^2}=\sum_{j=1}^{J}n_j\left(\frac{\bar{Y_j}-\bar{Y}}{\sigma}\right)^{2}=\sum_{j=1}^{J}\left(\frac{\bar{Y_j}-\bar{Y}}{\sigma/\sqrt{n_j}}\right)^{2} \sim \chi^2(J-1)$$
Nous faisons en effet dans cette expression la somme de $J$ (ici $J=2$) carrés de lois normales centrées (par soustraction des moyennes de groupe empiriques $\bar{Y_j}$) et réduites, indépendantes. La loi est une $\chi^2$ mais à $J-1$ (ici $J-1=1$) degrés de liberté, une fois soustrait le degré imputable au remplacement de la moyenne vraie $\mu$ inconnue par son estimation $\bar{Y}$.
Par ailleurs, la déviance de $M_1$ divisée par la variance vraie des données a aussi une distribution connue : $$\frac{D_1}{\sigma^2}=\sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(\frac{Y_{ij}-\bar{Y_j}}{\sigma}\right)^{2}\sim \chi^2(N-2)$$
Nous faisons en effet dans l'expression précédente une somme de $n_1+n_2=N$ termes, qui sont tous des scores centrés et réduits. La distribution est $\chi^2$ si on pense que les scores sont issus d'une population normale. On retranche néanmoins $J$ (ici $J=2$) degrés de liberté car le centrage a été réalisé par rapport à $J$ moyennes estimées, en lieu et place des moyennes vraies inconnues.
Bien sûr, dans ces deux expressions, nous manipulons un paramètre $\sigma^2$ de variance inconnue, mais la construction de Fisher nous permet de nous en affranchir. En faisant le rapport de ces deux statistiques, préalablement divisée par leurs degrés de liberté, on a : $$\begin{aligned} F&=\frac{R_{01}/\sigma^2/(J-1)}{D_{1}/\sigma^2/(N-J)} \\ &=\frac{\left[\sum_{j=1}^{J}n_{j}\left(\bar{Y}_{j}-\bar{Y}\right)^{2}\right]/(J-1)}{\left[\sum_{j=1}^{J}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y}_{j}\right)^{2}\right]/(N-J)}\sim Fisher(J-1,N-J) \end{aligned} $$
Cette statistique, nommée $F$ de Fisher, permet de juger du caractère significatif de la réduction de la déviance apportée par le modèle $M_1$, par rapport à ce qu'est la déviance de $M_0$, dans ce cas simple à deux moyennes. Mais elle peut en réalité être utilisée pour tester la réduction de la déviance apportée par n'importe quel modèle (à 2, 3, etc. moyennes) par rapport à un modèle plus simple. C'est ce que nous verrons dans la section suivante.
Dans le cas présent où nous n'avons que deux groupes ($J=2$), la statistique et la distribution de référence deviennent : $$F=\frac{\left[\sum_{j=1}^{J}n_{j}\left(\bar{Y}_{j}-\bar{Y}\right)^{2}\right]/(1)}{\left[\sum_{j=1}^{2}\sum_{i=1}^{n_{j}}\left(Y_{ij}-\bar{Y}_{j}\right)^{2}\right]/(N-2)}\sim Fisher(1,N-2) $$
Atelier
R2STATS calcule automatiquement les déviances, la réduction, le $F$ de Fisher et la valeur $p$ associés :
- Rechargez le fichier guyer0.csv dans R2STATS.
- Testez le modèle $M_0$, en sélectionnant correctement la variable dépendante et en entrant dans la boite des variables indépendantes le code '1'. Le symbole '1' sert à représenter une "variable" qui ne contient que des 1 (en réalité une constante). Le logiciel comprend alors que nous voulons tester un modèle prévoyant la même valeur constante de performance pour tous les sujets.
- Testez le modèle $M_1$, en sélectionnant correctement la variable dépendante et la variable indépendante.
- Dans la page des résultats, sélectionnez M0 et M1 dans la liste des modèles et cliquez sur le bouton Comparer : vous obtenez automatiquement un tableau de comparaison des déviances de $M_1$ et de $M_0$.
- Repérez dans le tableau de comparaison des déviances les valeurs de déviance de chaque modèle. Repérez ensuite la valeur de réduction de la déviance, le $F$ de Fisher associé et la valeur $p$ correspondante.
-
expand_moreEn résumé
Cet exercice a permis de mettre en oeuvre la comparaison de modèles par réduction de déviance (aussi appelée Analyse de la Variance ou ANOVA en abrégé) :
- On peut constater que dans le cas de la comparaison de deux moyennes seulement, la valeur $p$ du test de Fisher est exactement la même que celle du $T$ de Student de comparaison de deux moyennes. La conclusion est donc identique : nous déclarons les deux moyennes significativement différentes (en pratique, on observe plus de coopération dans le groupe où la décision est publique).
- On peut constater également que la valeur du $F$ de Fisher est égale au carré du $T$ de Student. Dans le cas à deux groupes, les deux statistiques donnent donc exactement la même conclusion. Attention cependant : le $F$ de Fisher révèle éventuellement une différence, mais de façon non signée (il est toujours positif) et le test est donc bilatéral par défaut.
- L'approche par analyse de la déviance a l'avantage cependant de permettre de comparer un nombre quelconques de moyennes, ce qui n'était pas possible avec le $T$. Dans ce contexte, les notions d'unilatéral et de bilatéral perdent leur sens : le $F$ est multilatéral par nature (il révèle toute différence perceptible entre un nombre quelconque de moyennes).
- Pour peu que la variable dépendante soit bien la même, cette approche permet de comparer n'importe quelle paire de modèles.
Test de contrastes locaux
Pour illustrer la possibilité de comparer un nombre quelconque de modèles différents sur la même variable dépendante, nous éudions ci-dessous la comparaison simultanée de 5 moyennes par cette approche.
Une expérience : rappel et contexte d'apprentissage
Dans une réplique d'une expérience de Smith (1979), on souhaite mettre en évidence l'effet facilitateur du contexte d'acquisition sur le rappel. Dans un premier temps, les sujets apprennent une liste de quatre-vingts mots dans une pièce orange décorée avec des draperies, posters, et tableaux. Les sujets subissent quelques minutes après leur apprentissage un test de reconnaissance dont le but est simplement de leur laisser croire que l'expérience s'arrête là. Le lendemain, on demande aux sujets de noter les mots dont ils peuvent se souvenir, et on les compte.
Le rappel se déroule dans différentes conditions qui définissent cinq groupes expérimentaux (les sujets étant affectés aléatoirement à chaque groupe) :
- Même contexte : les sujets se trouvent dans la même pièce orange où ils ont appris la liste la veille.
- Contexte différent : les sujets se trouvent dans une pièce nettement différente de celle où ils ont appris la veille.
- Contexte imaginé : les sujets sont dans la pièce du groupe (2). Mais on leur conseille de se rappeler d'abord la pièce orange (on les aide en leur posant des questions).
- Contexte photographié : les sujets se trouvent dans la condition (3), mais on leur montre plusieurs photographies de la pièce orange.
- Contexte placebo : les sujets sont dans la même pièce que le groupe (2). Mais on leur demande de se rappeler d'abord leur chambre à coucher à titre « d'échauffement intellectuel ».
Dans cette situation, on s'attend à ce que la proximité entre les conditions de l'apprentissage et les conditions du rappel favorise la performance au rappel. Si cette hypothèse est correcte, on devrait observer de meilleures performances en moyenne quand le rappel a lieu dans le même contexte que l'apprentissage. Il se peut aussi que si l'on réactive les conditions de l'apprentissage avec une photo, ou une consigne d'imaginer le contexte, la performance soit meilleure que lorsque le contexte est franchement différent. Ce sont ces différentes nuances de l'effet que l'on cherche à évaluer.
Atelier
Les données sont dans le fichier contexte2.csv. Testez sous R2STATS les modèles qui affirment les choses suivantes :
- $M_c$ : les cinq conditions se distinguent dans leurs effets moyens sur le rappel. Testez les conditions d'application du modèle de groupe. Examinez et interpréter les effets du tableau final des paramètres estimés. Note : ces effets sont tous calculés par rapport à la moyenne du groupe de base Placebo.
- $M_3$ : les cinq conditions diffèrent sauf les conditions « placebo » et « contexte différent » qui ne se distinguent pas entre elles.
- $M_2$ : les conditions « placebo » et « contexte différent » ne se distinguent pas entre elles, et les conditions « même » et « photographié » ne se distinguent pas entre elles.
- $M_1$ : aux deux précédentes contraintes d'égalité, on ajoute enfin que la condition 3 ne se distingue pas de la 1 et de la 4.
- $M_0$ : les cinq conditions ne se distinguent pas entre elles.
Utilisez pour cela les facteurs de groupe simplifiés f1, f2 et f3, fournis dans le fichier de données. Chacun d'entre eux représente l'une des hypothèses possibles sur la structure de groupe sous-jacente, selon qu'on considère réelle ou non certaines différentes de moyennes. Ils peuvent être utilisés tour à tour comme variable indépendante, en lieu et place du facteur Condition de départ.
Il représentent les hypothèses statistiques suivantes sur les moyennes (ou les indices représentent les numéros de groupes fusionnés dans l'hypothèse) :
| Condition / Modèle | $M_c$ | $M_3$ | $M_2$ | $M_1$ | $M_0$ |
|---|---|---|---|---|---|
| Même contexte | $\mu_{1}$ | $\mu_{1}$ | $\mu_{14}$ | $\mu_{134}$ | $\mu_{12345}$ |
| Contexte différent | $\mu_{2}$ | $\mu_{25}$ | $\mu_{25}$ | $\mu_{25}$ | $\mu_{12345}$ |
| Contexte imaginé | $\mu_{3}$ | $\mu_{3}$ | $\mu_{3}$ | $\mu_{134}$ | $\mu_{12345}$ |
| Contexte Photographié | $\mu_{4}$ | $\mu_{4}$ | $\mu_{14}$ | $\mu_{134}$ | $\mu_{12345}$ |
| Contexte placebo | $\mu_{5}$ | $\mu_{25}$ | $\mu_{25}$ | $\mu_{25}$ | $\mu_{12345}$ |
-
expand_moreCorrection
Cet exercice a permis de mettre en oeuvre la comparaison de modèles par réduction de déviance, dans le cas de 5 moyennes, avec tests sur contrastes.
- On teste d'abord le modèle complet $M_c$, c'est-à-dire celui qui teste l'effet global de la condition, sans introduire de contrainte. Ce modèle complet doit toujours être testé en premier car c'est celui qui nous donne le grain le plus fin sur les éventuelles différences de groupe. C'est aussi celui dont la déviance va être prise comme référence pour le calcul de tous les $F$ de Fisher de la table des comparaisons. A ce titre, c'est lui qui sert de base pour les tests d'homogénéité des variances et de normalité (qui ne seront pas testés sur les autres modèles).
On note que ces deux hypothèses du modèle de groupe sont acceptables ici, car le deux valeurs $p$ des tests de normalité et d'homogénéité des variances sont supérieures à $\alpha=0.10$ ($W = 0.96248, p < 0.2710$ et $F = 0.22168, p < 0.9242$). Remarque : le $F$ de Levene est un test d'homogénéité des variances approprié quand on a plus de deux variances. Sa lecture et son interprétation sont exactement identiques au $F$ de Fisher pour deux variances.
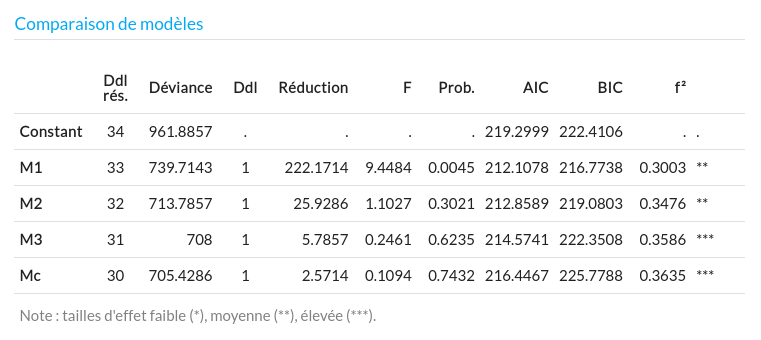
- On cherche maintenant à se convaincre qu'il y a bien de la différence quelque part entre les moyennes. Si c'est vrai, on devrait avoir une réduction de déviance significative quand on compare M0 (modèle constant) et Mc (modèle complet). Dans l'onglet Résultats, cliquez sur Mc puis sur le bouton Comparer : un tableau des déviances apparaît en bas de page. On voit que la déviance de Mc ($D_c=705.4286$) est plus faible que celle de M0 ($D_0=961.8857$) et que la différence entre les deux ($R_{c0}=256.4571$) est significative ($F=2.7266, p < 0.0477$). On peut donc dire qu'il y a un effet global significatif de la similarité du contexte sur la qualité du rappel.
- On cherche maintenant à identifier dans quel sens (favorisant / défavorisant) va cet effet, et entre quels groupes il est le plus notable. On va regarder le graphique des moyennes (onglet Graphiques). Deux moyennes sont particulièrement proches l'une de l'autre : celles des groupes 2 et 5 (Différent et Placebo). Il se peut qu'un modèle ne les distinguant pas amène pratiquement la même réduction de déviance par rapport à $M_0$. On teste ce modèle $M_3$ en remplaçant le facteur Condition par le facteur f3 du fichier, qui ne compte que 4 modalités de groupe (car les groupes 2 et 5 y ont été fusionnés). C'est ce qu'on appelle fixer une contrainte d'égalité dans un modèle de moyennes. Quand on compare entre eux $M_c$, $M_3$ et $M_0$, on constate que $M_3$ amène une réduction de déviance significative par rapport à $M_0$ ($F=3.599, p < 0.0248$) mais que $M_c$ n'apporte pas de gain explicatif (ou de réduction de déviance) significatif par rapport à $M_3$ ($F=0.1094, p < 0.7432$). $M_3$ est donc pour nous un meilleur modèle que $M_c$, avec une réduction de déviance à peu près équivalente et une structure de moyennes plus simple.
- Cela dit, quand on regarde les moyennes au sein du modèle $M_3$, on note que les moyennes des groupes 1 et 4 sont plutôt proches, et on peut souhaiter les mettre à l'épreuve. Il se peut en effet qu'un modèle intermédiaire, plus simple que $M_3$ suffise à réduire significativement la déviance par rapport à $M_0$, et que ni $M_3$ ni $M_c$ ne fassent significativement mieux. On teste le modèle $M_2$ correspondant à cette nouvelle contrainte $\mu_1=\mu_4$. Il apporte une réduction de déviance significative par rapport à $M_0$, et ni $M_3$ ni $Mc$ ne réduisent ensuite significativement sa déviance. C'est donc notre meilleur modèle dans cette situation.
- Un raisonnement semblable nous amène à réaliser qu'un modèle $M_1$ fixant l'égalité supplémentaire $\mu_3=\mu_{14}$ amène une réduction significative de la déviance ($F=9.4484, p < 0.0045$) et que ni $M_2$, ni $M_3$, ni $M_c$ n'apportent ensuite de réduction supplémentaire significative. $M_1$ est donc le meilleur de nos modèles dans cette situation. Les 5 conditions expérimentales se réduisent en fait à deux clusters de groupes : (134) d'une part, et (25) d'autre part.
- Une fois le meilleur modèle identifié, on l'inteprète : on voit que dans les groupes 1, 3 et 5 (où la proximité de contexte est élevée), le score moyen de rappel est plus élevé que dans les conditions 2 et 5 (où la proximité de contexte est nulle). Il y a donc bien un effet favorisant de la similarité de contexte sur le rappel.
- Remarque importante : pour que toute cette démarche de comparaison de modèles par valeur $p$ soit valide, il est important que toute contrainte d'égalité acceptée à une étape soit maintenue aux étapes suivantes. De cette manière, chaque contrainte vient tester un effet qui n'a pas encore été testé (notion de contrastes orthogonaux). Pour la facilité de l'inteprétation, on commence par contraindre les plus petites différences de moyennes, puis les plus grandes.
- On teste d'abord le modèle complet $M_c$, c'est-à-dire celui qui teste l'effet global de la condition, sans introduire de contrainte. Ce modèle complet doit toujours être testé en premier car c'est celui qui nous donne le grain le plus fin sur les éventuelles différences de groupe. C'est aussi celui dont la déviance va être prise comme référence pour le calcul de tous les $F$ de Fisher de la table des comparaisons. A ce titre, c'est lui qui sert de base pour les tests d'homogénéité des variances et de normalité (qui ne seront pas testés sur les autres modèles).
Exercices d'application
- Reprenez l'exemple des scores QI par groupe de genre (fichier wais2.csv), dans l'interface R2STATS, et vérifiez les deux
points suivants :
- Le $F$ de Fisher fourni dans la page des résultats est (dans ce cas particulier à deux groupes) exactement égal au carré du $T$ de Student.
- La valeur $p$ du test de Fisher est exactement celle du $T$ de Student.
-
Téléchargez le fichier anorexie.csv. Il contient les poids (en livres car l'étude est anglaise) avant et après traitement (suivi 3 mois) de 3 groupes indépendants de jeunes femmes anorexiques, suivies respectivement en a) hospitalisation classique, b) thérapie cognitive-comportementale, c) thérapie familiale. On admettra que les poids initiaux (PoidsAvant) des patientes dans les 3 conditions ne se distinguaient pas en moyenne. Les 3 types d'accompagnement ont-ils la même efficacité ? On regardera pour en juger uniquement la variable dépendante PoidsApres (poids après traitement).
- Y a-t-il globalement un impact du mode d'accompagnement, quel qu'il soit, sur la reprise de poids ? On testera les conditions d'application de la méthode choisie au préalable.
- Analyse de contraste : peut-on dire que les deux méthodes de psychothérapie diffèrent significativement quant à leur efficacité ?
-
expand_moreCorrection
-
On vérifie facilement que :
- dans cette analyse, la comparaison de $M_1$ et $M_0$ donne $F(1,58)=1.5539$ et que le simple $t$ de Student, apparaissant à la ligne SexeM du tableau des coefficients est $t(58)=-1.2466$. A l'arrondi près, on a bien $t^2=F$.
- la valeur $p$ ($p < 0.2176$) est la même dans les deux approches. Dans le cas de deux groupes, l'approche par comparaison des déviances (ou analyse de la variance) donne exactement la même décision et correspond au même modèle de groupe (avec hypothèse de normalité et d'homogénéité des variances). L'avantage de l'ANOVA n'apparaît que lorsqu'on commence à vouloir comparer plus de deux groupes.
-
On commence par tester le modèle complet $M_c$, supposant que les 3 populations sous-jacentes, dont les groupes sont issus, n'ont pas la même moyenne vraie de reprise de poids après traitement. Ce modèle est caractérisé par un triplet de moyennes vraies différentes qu'on peut noter $(\mu_1,\mu_2,\mu_3)$. L'estimation des 4 paramètres de ce modèle (3 moyennes estimées et une erreur standard commune) permettent de tester les hypothèse de normalité ($W = 0.98419$, $p < 0.5036$) et d'homogénéité des variances ($F = 1.76713$, $p < 0.1785$) : les deux tests ne conduisent au rejet d'aucune des deux et on considérera donc que ces conditions sont acceptables. On peut donc poursuivre l'analyse.
- La réponse à la première question (y a-t-il globalement un effet inter-groupe ?), sans chercher à localiser l'effet pour l'instant, suppose une comparaison du modèle de la différence $M_c$ avec un autre modèle qui affirme l'absence d'effet ($M_0$). Cette comparaison est réalisée automatiquement dans R2STATS quand on sélectionne le modèle $M_c$ dans la liste de l'onglet Résultats, et qu'on clique sur le bouton Comparer (en l'absence d'autres modèles sélectionnés, la comparaison se fait toujours implicitement avec le modèle constant de l'absence d'effet, $M_0$). On obtient une réduction de déviance significative apportée par $M_c$ par rapport à $M_0$ ($R_{c0}=918.9869$, $F(2,69)=8.6506$, $p < 0.0004$). On conclut donc à une différence significative globale des moyennes de reprise de poids (sans localisation de l'effet pour l'instant).
-
Le test d'un effet de la psychothérapie, sans distinction des deux formes de psychothérapie, peut être réalisé en construisant un modèle $M_1$ où les groupes TCC et TF sont fusionnés en un seul (voir le groupe Traitement, défini dans la colonne c1 du fichier de données). On note que ce modèle peut nous apprendre deux choses différentes, selon la comparaison que l'on fait ensuite : comparer $M_1$ et $M_c$ permet de répondre à la question de savoir si les deux formes de psychothérapie se distinguent en efficacité (car c'est la seule distinction qui change de $M_1$ à $M_c$), et comparer $M_1$ à $M_0$ permet de mettre en évidence un effet psychothérapie global, sans distinction de forme (car l'opposition Contrôle / Traitement est la seule chose qui change de $M_0$ à $M_1$). On dit que ces 3 modèles sont emboîtés les uns dans les autres, car on obtient $M_1$ en fixant l'égalité $\mu_2=\mu_3=\mu_{23}$ dans $M_c$, et on obtient $M_0$ en fixant $\mu_1=\mu_{23}$ dans $M_1$. Que les modèles soient ainsi emboîtés est une condition indispensable pour l'usage des $F$ de Fisher de comparaison de déviance, car ceux-ci viennent tester l'apport spécifique d'une distinction nouvelle, apportée par un modèle, par rapport au modèle précédent dans la série, qui sert de point de comparaison (on verra plus loin comment comparer des modèles qui ne respecteraient pas cette condition d'emboîtement).
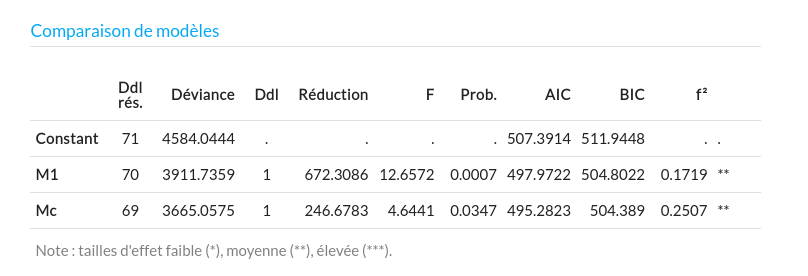
Pour la comparaison de $M_0$ et de $M_1$, on trouve une réduction de la déviance de $R_{10}=672.3086$, significative ($F(1,69)=12.6572$, $p < 0.0007$). La distinction du groupe contrôle et des conditions de psychothérapie (sans distinction de formes) permet donc de mieux rendre compte de la différence inter-groupe. La comparaison de $M_1$ et $M_c$ fait apparaître également une réduction significative de la déviance de $R_{10}=246.6783$, significative ($F(1,69)=4.6441$, $p < 0.0347$). Au-delà de l'effet global de la psychothérapie, la distinction des deux formes (TCC et TF) permet encore d'améliorer l'explication de la différence inter-groupe. On dira que $M_c$ est un modèle significativement meilleur que $M_1$ dans l'explication des résultats, et c'est donc lui que nous sélectionnons ici comme le meilleur modèle.
Les conclusions d'une analyse par modélisation sont toujours les éléments de structure du meilleur modèle retenu : $M_c$ suppose la différence des 3 conditions entre elles, et c'est donc notre conclusion statistique. Pour interpréter psychologiquement ce résultat, on regarde les paramètres (ou coefficients) estimés de $M_c$. On peut voir dans le tableau correspondant qu'au delà du poids moyen final des patientes du groupe contrôle ($\bar{x}_1=81.1077$ livres), les patientes du groupe TCC ont obtenu un différentiel de reprise de poids de $\bar{x}_2-\bar{x}_1=4.5889$ supplémentaire (autrement dit $\bar{x}_2=85.6966$ livres). Les patientes du groupe TF ont obtenu un différentiel de reprise de poids de $\bar{x}_3-\bar{x}_1=9.3864$ supplémentaire (autrement dit $\bar{x}_3=90.4941$ livres). La thérapie familiale fait donc mieux que la thérapie cognitivo-comportementale, et la TCC mieux que le groupe contrôle (un résultat classique sur les troubles alimentaires).
-