Distribution d'une variance

Nous comprenons dans cette expérience que lorsque nous réalisons une étude et résumons ses résultats par une moyenne et une variance empiriques, ces deux statistiques sont en réalité des réalisations particulières de variables aléatoires plus générales que nous notons $\bar{X}$ et $S^2$ (en majuscules, pour marquer dans l'écriture qu'il ne s'agit pas de nombres).

Estimation de la variance

Une variance d'échantillon peut se calculer de deux manières, selon que l'on connaît ou non la moyenne vraie $\mu$ du phénomène. Si on la connaît, on peut calculer : $$S_{\mu}^{2}=\frac{\sum_{i=1}^{N}(X_{i}-\mu)^{2}}{N}$$ Si on ne la connaît pas, on utilise la variance descriptive, vue en première année, qui s'écrit : $$S_{\bar{X}}^{2}=\frac{\sum_{i=1}^{N}(X_{i}-\bar{X})^{2}}{N}$$ On note que sous cette deuxième forme, l'indice de variance est soumis à la fois à sa propre erreur d'échantillonnage (elle est calculée sur un échantillon), et à l'erreur d'estimation de la moyenne $\bar{X}$. C'est en effet une particularité de la variance : nous avons besoin de la moyenne pour la calculer (l'inverse n'est pas vrai). Quelle que soit la forme utilisée, nous devons nous convaincre qu'elles ne sont pas une trop mauvaise mesure de la vraie variance inconnue $\sigma^2$.

En particulier, même si sur un échantillon donné nous savons bien que $s^{2}\neq\sigma^{2}$, nous aimerions assez que la variance d'échantillon, en moyenne sur une infinité d'échantillons (c'est-à-dire en espérance), égale la variance vraie (propriété dite de « non-biais » dont dispose la moyenne d'échantillon, comme nous l'avons vu), c'est-à-dire : $$E\left[S^2\right]=\sigma^2$$ C'est ce que nous étudions dans l'atelier suivant.

Atelier 1 : biais de l'estimateur de variance

Dans cet atelier, on prélève un certain nombre d'échantillons de taille fixée dans une population de loi normale de moyenne 0 et d'écart-type 1. Sur chaque échantillon on calcule la variance. Ce sont ces valeurs de statistiques variance qui sont représentées sous forme d'un histogramme de distribution. La valeur $m(S^2)$ qui s'affiche permet de percevoir la valeur centrale de cette distribution empirique (et le trait pointillé orange vertical permet de la visualiser graphiquement). On cherche à voir si la variance calculée sur l'échantillon n'est pas trop éloignée de la variance vraie réglée ici à 1 dans le simulateur (et matérialisée par la ligne verticale orange pleine).

• expand_moreEn résumé

  En répondant aux questions de cet exercice, vous avez pu constater que :

  • la variance calculée avec moyenne vraie est une statistique sans biais : $$E(S^{2}_{\mu})=\sigma^2$$ Néanmoins, dans un certain nombre de cas, nous aurons besoin d'utiliser une estimation de la variance sans avoir connaissance de la moyenne vraie, et sans vouloir faire d'hypothèse sur elle. Nous la calculerons alors avec une estimation de la moyenne.
  • Mais la variance calculée avec la moyenne estimée $\bar{X}$ apparaît biaisée. Plus précisément, son espérance est (voir Manuel de cours, section 9.3.1, p. 208) : $$E(S^{2}_{\bar{X}})=\sigma^2-\frac{\sigma^2}{N}$$ Elle est donc systématiquement trop petite.

    Sans démonstration, il est possible de comprendre ce phénomène en observant la représentation ci-contre.

    Pour mesurer la dispersion des notes au sein d'un échantillon, la variance fait la moyenne des carrés des écarts à la moyenne. On voit qu'en calculant ces écarts par rapport aux moyennes empiriques ($\bar{x}_{i}$, représentées ci-contre par des triangles), nous aurons des valeurs plus petites que par rapport à la vraie valeur centrale $\mu$. La quantité de variance qui manque dans le calcul pour chaque échantillon est l'écart (carré) de son $\bar{x}_i$ à la vraie valeur de moyenne $\mu$.

    En espérance, sur l'ensemble de tous les échantillons possibles, la part de variance ignorée dans ce calcul est très exactement la variance des $\bar{x}_i$, c'est-à-dire $\frac{\sigma^{2}}{N}$ (revoir au besoin la section Distribution d'une moyenne d'échantillon).

    Calculer une variance avec la moyenne d'échantillon comme point central, c'est en quelque sorte décider d'ignorer que la moyenne d'échantillon est une variable aléatoire, et non une valeur vraie, et par conséquent ignorer sa variabilité propre.

    

Correction de l'estimateur de variance

La variance calculée avec la moyenne empirique est donc biaisée. On peut réécrire son espérance comme : $$E(S^{2}_{\bar{X}})=\sigma^2-\frac{\sigma^2}{N}=\sigma^2\left[{\color{Cyan}1}-\frac{1}{N}\right]=\sigma^{2}\left[\frac{{\color{Cyan}N}-1}{{\color{Cyan}N}}\right]$$ Cela suggère de corriger l'estimateur $S_{\bar{X}}^{2}$ sous la forme inversement corrigée : $$\tilde{S}_{\bar{X}}^{2}=\left[\frac{N}{N-1}\right]S_{\bar{X}}^{2}=\left[\frac{{\color{Cyan}N}}{N-1}\right]\frac{\sum_{i=1}^{N}(X_{i}-\bar{X})^{2}}{{\color{Cyan}N}}=\frac{\sum_{i=1}^{N}(X_{i}-\bar{X})^{2}}{N-1}$$

Une interprétation possible du phénomène de biais de la variance est qu'en prenant la moyenne estimée comme point de référence central du calcul de variance, et en choisissant d'ignorer sa variabilité d'estimateur, tout à l'air de se passer comme si nous avions perdu une observation.

Exercice. On vérifie facilement à l'aide du simulateur précédent, en cochant l'option « Variance corrigée », que cet estimateur corrigé remplit bien son office, c'est-à-dire que : $$E\left[\tilde{S}_{\bar{X}}^{2}\right]=\sigma^2$$ C'est désormais le seul estimateur de variance que nous utiliserons.

La loi de $\chi^2$

Atelier 2 : découverte des propriétés de la loi de $\chi^2$

Dans cet atelier, on simule le processus de construction d'une loi de $\chi^2$, en tirant $N$ valeurs dans une loi normale $N(0,1)$, et en additionnant les carrés de ces valeurs. En changeant le nombre $N$ de valeurs sommées (nommé nombre de composantes ci-dessous), on voit apparaître certaines propriétés.

• expand_moreEn résumé

  A partir de cet exercice, nous comprenons :

  • que la moyenne d'une loi de $\chi^2$ est simplement son nombre de degrés de liberté, c'est-à-dire le nombre de composantes normales standard carrées additionnées dans sa construction.
  • que la variance de cette loi est deux fois son nombre de degrés de liberté.
  • que la loi de $\chi^2$ tend vers la loi normale quand son nombre de degrés de liberté tend vers l'infini. La loi de $\chi^2$ est en effet la loi d'une somme de variables indépendantes de même distribution initiale (des lois normales standard carrées). Elle tombe donc sous le coup du théorème central limite.
  • qu'une somme de variables $\chi^2$ est elle-même une variable $\chi^2$ dont les degrés de liberté sont simplement la somme des degrés de liberté des $\chi^2$ additionnées.

Lien de la loi de $\chi^2$ avec la statistique variance

Cas n°1 : moyenne vraie connue

Si la variance est calculée avec moyenne connue, elle s'écrit : $$S_{\mu}^{2}=\frac{\sum_{i=1}^{N}(X_{i}-\mu)^{2}}{N}$$ En manipulant un peu cette expression, on fait apparaître que : $$N\times\frac{S_{\mu}^{2}}{{\color{Cyan}\sigma^{2}}}=\frac{\sum_{i=1}^{N}\left(X_{i}-\mu\right)^{2}}{{\color{Cyan}\sigma^{2}}}=\sum_{i=1}^{N}\left(\frac{X_{i}-\mu}{{\color{Cyan}\sigma}}\right)^{{\color{Cyan}2}}$$ Si les $X_i$ suivent des lois normales, leur version standard suit une loi normale centrée réduite, et la variance transformée $N\times\frac{S_{\mu}^{2}}{\sigma^{2}}$ apparaît comme une somme de carrés de loi normales centrées réduites, indépendantes si les données ont été collectées indépendamment. Elle suit donc par définition une loi de $\chi^2$ à $N$ degrés de liberté : $$N\times\frac{S_{\mu}^{2}}{\sigma^{2}}\sim\chi^{2}(N)$$

Cas n°2 : moyenne vraie inconnue

Si on ne connaît pas la moyenne vraie (cas de loin le plus fréquent), ou qu'on ne souhaite pas faire d'hypothèse sur elle, on utilise la variance calculée avec $\bar{X}$ : $$S_{\bar{X}}^{2}=\frac{\sum_{i=1}^{N}(X_{i}-\bar{X})^{2}}{N-1}$$ et on observe que : $$\frac{(N-1)}{\sigma^{2}}S^{2}_{\bar{X}}=\frac{({\color{Cyan}N-1})}{\sigma^{2}}\sum_{i=1}^{N}\frac{(X_{i}-\bar{X})^{2}}{{\color{Cyan}N-1}}=\sum_{i=1}^{N}\left(\frac{X_{i}-\bar{X}}{\sigma}\right)^{2}$$ Bien que cette autre variance transformée soit elle aussi une somme de carrés de loi normales (si les données le sont) centrées réduites indépendantes (si la collecte ou la situation le garantit), nous devons garder en tête une particularité de la variance calculée avec $\bar{X}$ : elle introduit un biais qui a le même impact que la perte d'une observation.

Pour la variance transformée correspondante, nous avons bien une distribution $\chi^2$, mais avec un degré de liberté en moins (voir section 9.3 du manuel, p. 212, pour une démonstration formelle) : $$(N-1)\frac{S^{2}_{\bar{X}}}{\sigma^{2}}=\sum_{i=1}^{N}\left(\frac{X_{i}-\bar{X}}{\sigma}\right)^{2}\sim\chi^{2}(N-1)$$

Atelier 3 : test sur une variance par valeur $p$

Dans cet atelier, on peut utiliser directement le calcul de probabilités cumulées dans la loi de $\chi^2$ pour faire de l'inférence sur une variance inconnue, à partir d'une hypothèse. On saisit le nombre de degrés de liberté, puis une valeur de variance transformée et on obtient une valeur $p$. On choisit avec soin le sens du cumul selon l'orientation de l'hypothèse alternative.

Remarque pour la saisie des valeurs dans le champ « Quantile » : le calculateur sait interpréter les opérations (par exemple la fraction $4/2$) et peut faire le calcul pour vous. Le carré d'une valeur s'obtient en utilisant deux astérisques : par exemple « 2**2 » représente $2^2$.

• expand_moreEn résumé

  Cet exercice permet de dérouler les 5 étapes fondamentales de la démarche de test par valeur $p$, dans ce cas particulier de l'inférence sur une variance.

  1. Le type de problème posé est la comparaison d'une variance inconnue à une valeur normative.
  2. Les hypothèses statistiques sont : $$\begin{aligned} H_{0}:\sigma^{2} &= \sigma_{0}^{2}\\ H_{1}:\sigma^{2} & < \sigma_{0}^{2} \end{aligned}$$

     Dans ce contexte, l'hypothèse alternative $H_1$ est orientée à gauche et le calcul de la valeur $p$ devra donc se faire par cumul à gauche.

  3. La statistique de décision selon $H_{0}:\sigma^{2}=\sigma_{0}^{2}$, et sous hypothèse de normalité et d'indépendance des données, est : $$Q=(N-1)\frac{S^{2}}{\sigma_{0}^{2}}\sim\chi^{2}(N-1)$$ On calcule la variance transformée : $$q = 29\times\frac{14.5^{2}}{15^{2}}\approx 27.0988$$
  4. Conclusion statistique : l'alternative est unilatérale à gauche, et on définit une région critique de décision dans les valeurs les plus basses de la statistique. Dans le champ valeur, il est possible d'écrire directement la formule de calcul « 29*(14.5/15)**2 ». En choisissant une distribution de $\chi^{2}$ à $N-1=29$ degrés de liberté, on obtient facilement : $P(\chi^{2}(29) < 27.0988)\approx 0.433629$. Au seuil $\alpha=0.05$, cette probabilité est trop grande pour qu'on puisse rejeter l'hypothèse nulle.
  5. Conclusion psychologique : il n'est pas possible à partir de ces données de conclure que la variabilité est plus faible chez les étudiants que dans la population générale.

1. Dans une étude analogue à l'exercice modèle précédent, on trouve pour $N=25$ étudiants une variance empirique de $s^{2}=12.5^{2}$. Diriez-vous que la variance de scores QI chez ces étudiants est significativement plus faible que dans la population de référence (au seuil de décision $\alpha=0.05$) ?
2. Quelle valeur de variance empirique $s^{2}$ faudrait-il trouver pour conclure à une variabilité plus faible chez les étudiants ($\alpha=0.05$) ?

• expand_moreCorrection

  1. La question posée se traduit sur le plan statistique par la comparaison d'une variance inconnue $\sigma^2$ (la variance de scores QI chez les étudiants) à la norme connue du test $\sigma_0^2=15^2$.

     Dans une approche par valeur $p$, les deux hypothèses concurrentes sont : $$\begin{aligned} H_{0}:\sigma^{2} &= \sigma_{0}^{2}\\ H_{1}:\sigma^{2} & < \sigma_{0}^{2} \end{aligned}$$

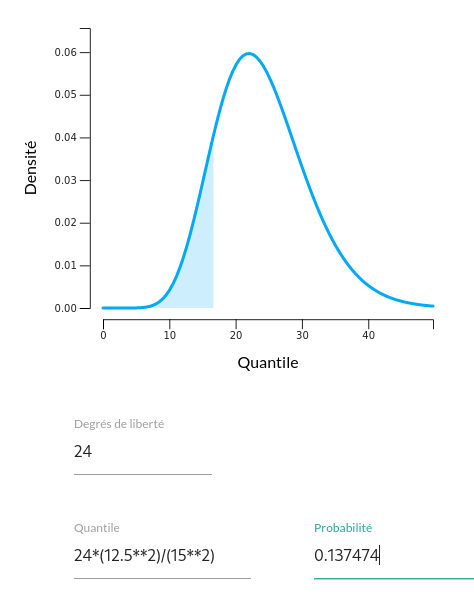
     La statistique de décision selon $H_{0}:\sigma^{2}=\sigma_{0}^{2}$, et sous hypothèse de normalité et d'indépendance des données, est : $$Q=(N-1)\frac{S^{2}}{\sigma_{0}^{2}}\sim\chi^{2}(N-1)$$ On calcule la variance transformée : $$q = 24\times\frac{12.5^{2}}{15^{2}}\approx 16.666$$ et le calculateur nous indique que : $$p=P(\chi_{24}^{2} < 16.666)\approx0.137$$ On a $p > 0.05$ et on ne peut donc rejeter l'hypothèse nulle. Il n'y a donc pas de raison de supposer une variabilité plus faible des scores d'intelligence chez les étudiants.

     
  2. Dans cette question, on cherche à trouver la valeur de la variance en-dessous de laquelle on concluera à une variance significativement plus faible que la norme. Cela revient à chercher le quantile $q$ (variance transformée) de la loi $\chi_{24}^{2}$ dont le cumul à gauche correspond au seuil de décision $\alpha=0.05$. A l'aide du calculateur, en saisissant la probabilité critique 0.05, on trouve facilement $q=13.84$, c'est-à-dire : $P(\chi_{24}^{2} < 13.84)=0.05$. On cherche donc $s^2$ tel que : $$(N-1)\frac{s^2}{\sigma^2} = 13.84$$ ou encore : $$s^2=\frac{13.848425\times15^2}{24}\approx 129.83=11.4^2$$ On concluerait donc à une variance significativement plus faible si on observait concrètement une valeur de variance empirique inférieure à $11.4^2$.